オペアンプで矩形波を増幅してみようと思います。
前にも同様のことをやっていますが、出力波形が台形になっていていました。スルーレートの影響のようなので確認してみたいです。前回、オペアンプ LM358 の電気的特性について調べてみていますが、そのときの測定ではスルーレートは 0.2V/μs でした。
周波数特性
オペアンプの周波数特性 (Frequency response) とは、入力する周波数を高くすると利得が小さくなる特性 (利得周波数特性) のこと。周波数が 10倍になると利得は -20dB (1/10) になります。利得と周波数の積を GB積 (Gain-bandwidth product) といい、GB積は一定値です。また、GB積は利得が 0dB (増幅率=1) のときの周波数 (ユニティゲイン帯域) です。
正弦波の場合、最大出力振幅が大きいと波形の傾きが大きくなりスルーレートを超えてしまうことがあります。そのため、周波数特性の測定はスルーレートの影響を受けないように小信号で行ないます。
データシートによると LM358 の GB積は 500KHz (VCC=10~15V) です。実験した回路の利得は 22.3 でしたので、数字上は 500/22.3=22.4[KHz] までこの利得で増幅することが可能です。が、矩形波のような傾きが大きい信号では、周波数特性よりもスルーレートに制限されることになります。
また、入力する周波数が高くなるほど出力波形に位相遅れを生じます (位相周波数特性)。位相が 180° 遅れると正帰還になってしまい、回路は不安定になり発振します。
単電源バイアス式非反転増幅回路
図1 のような簡単な単電源動作バイアス式の非反転増幅回路で矩形波信号を増幅してみます。
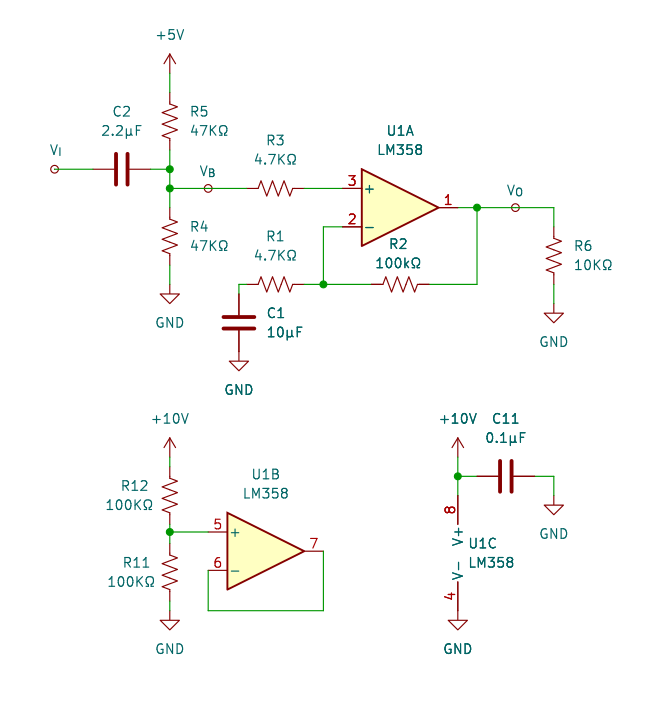
5V 電源を R4、R5 で分圧して 2.5V のバイアス電圧 VB を設定しています。クローズドループ利得 GV は、
GV = 1 + R2/R1 = 1 + 100 / 4.7 = 22.3
ですが、直流のバイアス電圧に対してはコンデンサ C1 があるために 1 です。出力電圧を 2.5V を中心とした±2V (0.5~4.5V) の振幅としたいので、オペアンプの電源電圧は 10V としました。
U1B は未使用なので、ボルテージフォロワにして電源の 1/2 の電圧を印加しておきます。
入力コンデンサ C2 は、R4、R5 とハイパスフィルタを構成します。R4=R5 のときカットオフ周波数 fC2 は、
fC2 = 1 / (2π・C1・R4/2) = 1 / (2π x 2.2 x 10-6 x 47 x 103 / 2 ) = 3.1 [Hz]
最低の周波数を 1KHz ほどとするならもっと小さな容量でもよさそうですね。C2 があることで入力信号は AC の扱いです。出力は Arduino に渡すと考えて DC のままですが、VB を中心にスイングすることになります。そのため、出力電圧が 0V 付近での動作遅れの影響がなくなります。
R4、R5 に流れる電流 IBR は、
IBR = V / 2・R4 = 5 / (2 x 47 x103) = 53.2 [μA]
入力バイアス電流 Ib (=250nA) の 200倍ほどです。ただし、この回路では 5V 電源が変動すると VB が直接影響を受けるため不安定になることがあります。留意しておきましょう。
入力インピーダンス ZI は、オペアンプの入力インピーダンスを無限大とすると、
ZI = R4/2 = 47 / 2 = 23.5 [KΩ]
R3 は入力オフセット電圧のキャンセル抵抗で、R1、R2 を並列としたときの抵抗値とします。
R3 = R1・R2 / (R1 + R2) = 4.7 x 100 / (4.7 + 100) = 4.49 [KΩ]
E6 系列から 4.7KΩ としました。
C1 は R1 とハイパスフィルタを形成します。カットオフ周波数 fC1 は、
fC1 = 1 / (2π・C1・R1) = 1 / (2π x 10 x 10-6 x 4.7 x 103) = 3.4 [Hz]
また、C1 のリアクタンス XC1 は R1 より十分小さくしておく必要があります。f=1KHz とすると、
XC1 = 1 / (2πf・C1) = 1 / (2π x 1 x 103 x 4.7 x 10-6) = 33.9 [Ω] ≪ 4.7 [KΩ]
C1 が小さいと波形が鋸状になります。大きすぎると応答が悪くなるようです。が、もう少し大きめの方が良いかもしれません。
毎度の俺的テキトーな計算ですけど、まぁそんなところ。いろいろ勉強しながらだんだん回路も良くなっていくでしょう、なったらいいな、と。
矩形波信号の入出力波形
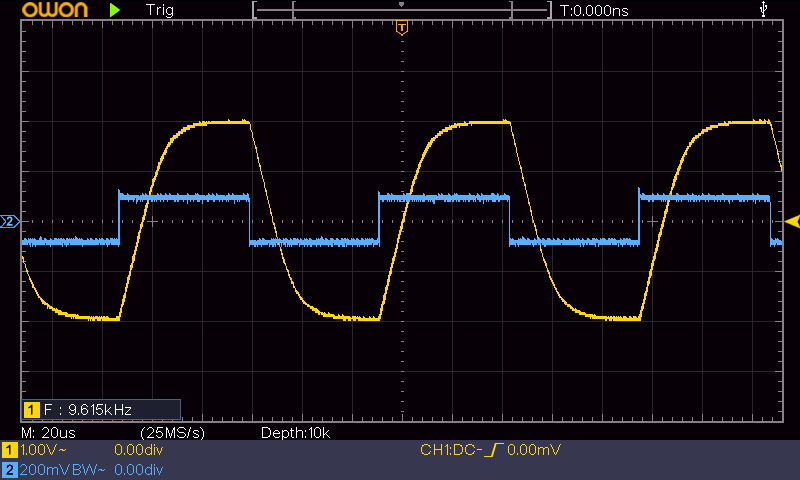
1.2KHz の矩形波信号を入力したときの入力 (青)、出力 (黄) 波形です。(図2)
入力電圧 180mVP-P、出力電圧 4VP-P で、増幅率は 22.2 です。スルーレートは 0.2V/μs で、出力波形が少し台形になります。C1 の影響で、わずかですが HIGH レベルが右下がり、LOW レベルが右上がりになっています。
が、おおむねきれいに増幅されています。
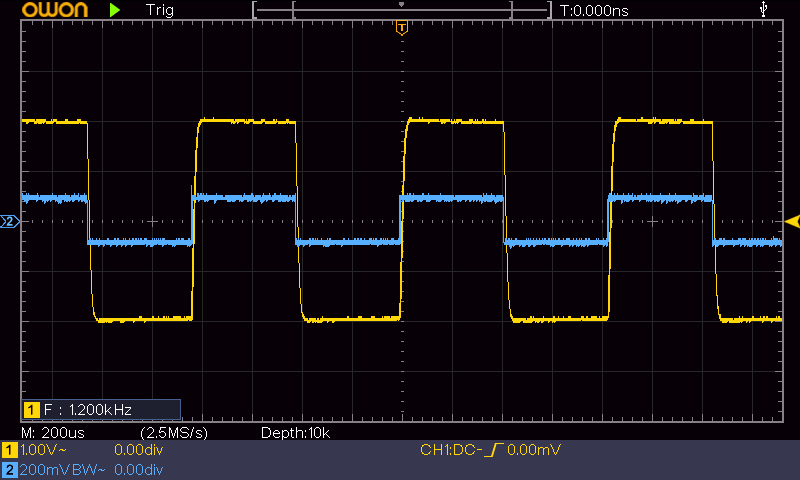
9.6KHz の矩形波信号の入出力波形です。(図3)
電圧レベルは 1.2KHz のときと同じです。が、スルーレートのために出力の立ち上がりがパルス幅の 1/2 ほどになってしまい、出力波形はかなり崩れてきます。位相も 30° 以上遅れています。
スルーレートは 0.2V/μs で、周波数には無関係です。
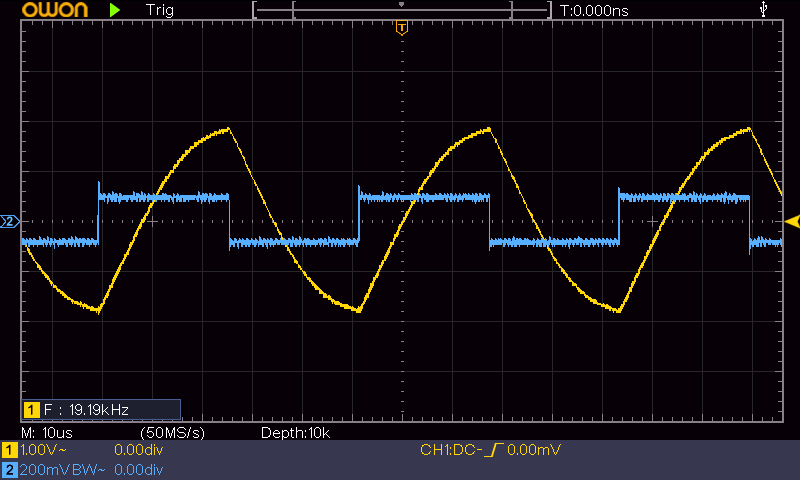
19.2KHz の矩形波信号の入出力波形です。(図4)
周期が 52μs で出力電圧が 3.6VP-P までしか立ち上がれないため、増幅率は 20 に減少しました。位相遅れも 60° 近くまで大きくなっています。
デジタル信号なら整形して使えそうですが、このあたりが限界でしょう。
正弦波信号の入出力波形
矩形波信号では周波数特性はスルーレートに制限されてしまいましたが、正弦波ではどうなのでしょう? ちょっと試してみました。
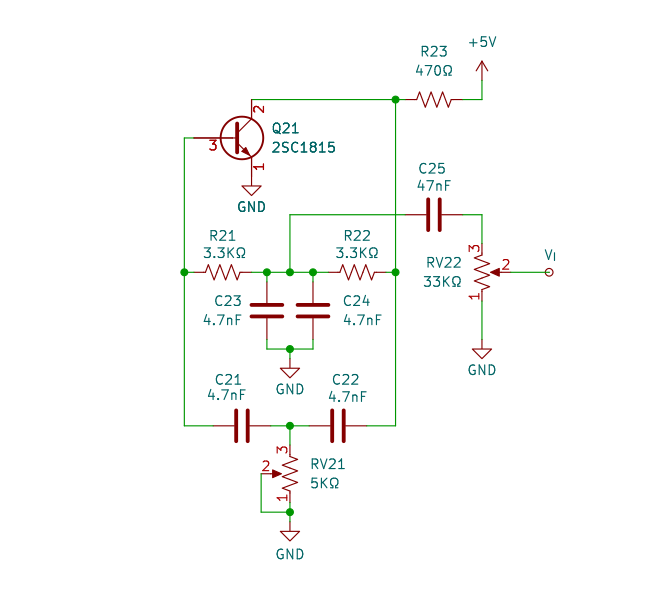
ツインT形正弦波発振回路
簡単に正弦波を発振させるためにツインT形発振回路を作りました。ツイン T形発振回路については、過去記事も参照ください。
図5 の定数で 13KHz~30KHz の正弦波が出力されました。RV21 で周波数が変化します。出力電圧は 450mVP-P (@16KHz) で、RV22 で調整します。
入出力波形
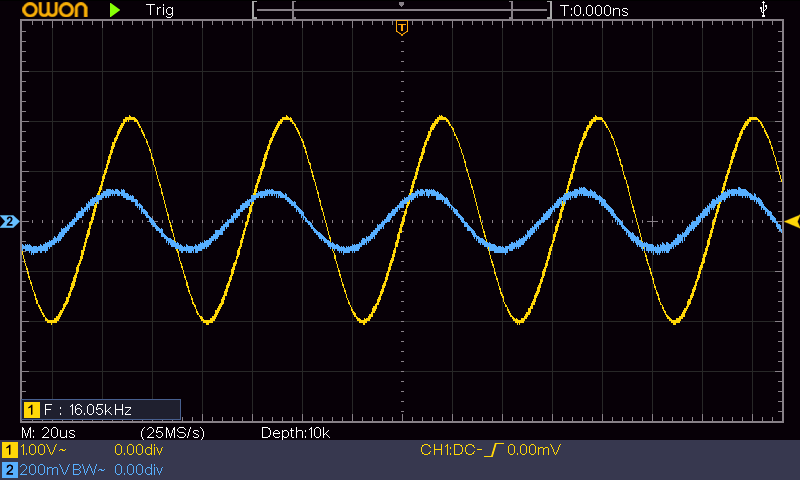
図6 は正弦波を入力したときの入出力波形です。
周波数 16KHz のとき入力電圧 220mVP-P で出力電圧 4.0VP-P、増幅率は 18.2 です。位相遅れは 40° ほどです。このとき出力信号の最大傾き S は、
S = 2πf・Vm = 2π x 16 x 103 x 2.0 = 0.20 [V/μs]
と、スルーレートと同じになりました。
周波数を上げていくとさらに増幅率が低下していきます。20KHz での増幅率は 13 程度で、出力波形が尖った感じになってきました。ここらあたりが限界のようです。LM358 で性能の良いヘッドホンアンプを作るのはちょっと難しいかもしれません。でも、電話のような 50~7000Hz の帯域なら十分ですので、無線機の低周波増幅器に使えそうです。
正弦波の最大傾き
正弦波の電圧 v は、最大電圧を Vm とすると、
v = Vm・sinωt
と表されます。なお、ω=2πf (f は周波数) です。この式を時間 t で微分すると、
v' = ωVm・cosωt
v’ は正弦波の傾きを表しており、これが最大になるのは ωt=0, π のときです。ωt=0, π のときの電圧 v は、
ωt = 0 のとき v = Vm・sin0 = 0 ωt = π のとき v = Vm・sinπ = 0
つまり電圧 v=0 のとき最大となり、その傾きは、
ωt = 0 のとき v'= ωVm・cos0 = ωVm ωt = π のとき v'= ωVm・cosπ = -ωVm
プラスの傾きは増加、マイナスは減少を表しますが、どちらも大きさは同じです。
後記
今回は、オペアンプ LM358 の単電源動作バイアス式の非反転増幅回路に矩形波を入力して、入出力波形をみてきました。出力電圧を大きくしようとすると、周波数特性ではなくスルーレートに制限されて入力周波数を高くすることができませんでした。正弦波では波形の傾きが小さくなりますので矩形波より有利ですが、出力を大きくすると高音域がつらそうです。
センサー信号の増幅用にと考えていたオペアンプ LM358 ですが、ちょっとした低周波増幅器にも使えそうですね。
さてと、オペアンプの超入門的なところはなんとなく理解できた感じです。一休みしたら、実際にセンサー出力を増幅する回路を考えてみましょうか。