「マクスウェルの方程式」を噛ってみた

電波とかアンテナとかを勉強しようとすると出てくる「マクスウェルの方程式」ですが、んな難しいことわかんねぇ〜よ。でも、ちょっと、噛じってみました。

な〜んもわからん俺の頭の中のマクスウェルの方程式なので、理論的とか数学的とか、ないです。あしからず。

パラメータ

まずは、電界、磁界に関するパラメータを復習しましょ。主なパラメータは次のとおりです。

電界

は電界。電場とも言います。ChatGPT によると、電界とは電荷が発生させる影響や力を伝える空間のこと、だそうです。
うーん？ 空間って何なのかわかりませんけど。俺の頭の中では「電界とは電気力線の本数」ってことになってます。電気力線は電荷 Q から出ます。電気力線の本数は誘電率 ε によって変化します。電気力線の本数は Q/ε [本] です。

ちなみに、上に矢印がついているのは、このパラメータがベクトルであることを示しています。つまり、空間に存在する影響や力を伝える何か、大きさと向きを持った量なのです。

磁界

は磁界。磁場とも言います。ChatGPT によると、磁界とは磁力が発生し影響を及ぼす空間のこと、だそうです。
えーとこれは「磁束密度を透磁率で割った値」のこと。電流が流れると磁束が生じるけど、同じ電流であっても磁束は透磁率によって変化します。そこで磁束 Φ を透磁率 μ で割ることで、透磁率に関係なく電流 I の値だけで決まる磁界 H って値が表せる。磁界 H=Φ/μ=I/2πr [A/m] と習いましたね。

電界の場合とちょっと違っているので、ややこしいです。言葉面に惑わされてはいけません。「電荷から電界が生じ、電界に誘電率を掛けたものが電束密度」です。「電流から磁束密度が生じ、磁束密度を透磁率で割ったものが磁界」なのです。ただし、ものによって用語もいろいろだったりして、さらにややこしいです。

電荷密度

電荷密度 は単位体積あたりの電荷の量。電荷を小さな小さな点のような体積に切り分けて (微分)、そこから出てくる電気力線の量を考えます。電気力線が出てくるということは電荷があるということです。

誘電率

真空中の誘電率 は電荷を蓄える能力といわれ、

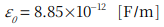
です。電荷を蓄える能力？ えーと、誘電率とは「電気力線の通りにくさ」を表しています。誘電率が大きいほど、電界は小さくなります。

透磁率

真空中の透磁率 は磁化のしやすさで、

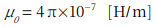
です。透磁率とは「磁束の通りやすさ」を表します。透磁率が大きいほど、磁束も大きくなります。

電束密度

電束密度 は単位面積あたりの電束の本数で、

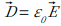
の関係となっています。Q [C] の電荷からは Q [本] の電束が出ます。Q [C] の電荷からでる電気力線の総本数は Q/ε₀ [本] です。つまり、電界は誘電率によって変化しますが、電束は変化しません。

磁束密度

磁束密度 は単位面積あたりの磁束の本数で、

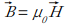
の関係があります。電流が流れると磁束密度が生じますが、磁束密度は透磁率によって変化します。磁束密度 B を透磁率 μ₀ で割った値が磁界 H=B/μ₀ で、磁界は電流の値だけで決まります。

伝導電流密度

伝導電流密度 は単位面積あたりの電流の密度。電流は 1秒間に流れる電荷の量、電流が単位面積を通過する量が伝導電流密度。伝導電流は磁界をつくります。なお、コンデンサのように電界の変化で流れる電流のことは変位電流といいます。変位電流も磁界をつくります。

電束密度でも磁束密度でもそうなんだけど、「単位面積あたり」とは、小さな小さな点のような面積 (微分) を垂直に通り抜ける成分 (法線ベクトル) だけを考えるので、ベクトルになる。電流や電束、磁束は大きさだけを表すのでスカラー。ああ、むずかしいっすねぇ (；´Д｀)

時間

は言うまでもなく流れゆく時間。

物事に時間が絡んでくるということは、時々刻々状態が変化するということ。状態を表す方程式はますます混迷を深め、難解になっていくのです。はぁ (；´Д｀)

電場に関するガウスの法則

初めは「電場に関するガウスの法則」です。

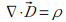
この式は「電荷から周囲へ電界が湧き出している」ことを示しています。ρ がプラスなら ＋電荷から電気力線が湧き出し、マイナスなら ー電荷へ電気力線が吸い込まれていることになります。

∇ (ナブラ) はベクトルで表され、

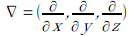
です。 は x 方向の変化率 (偏微分) を表します。y 方向、z 方向も同様です。
は ∇ と電束密度の内積をとるということで、電束密度の発散 (divergence) を表します。 とも表現します。なので、

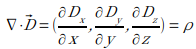
となって、電荷密度がある (右辺) ということは電束が空間内で変化する (左辺) ということを示します。つまり、電束が発散する、電界が湧き出す、ってこと。

ちなみに、ベクトルとベクトルの内積はスカラーになるので、電荷密度 ρ はスカラーです。

磁場に関する法則

つぎに「磁場に関する法則」です。

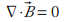
この式は「磁極は N極と S極が対になっており、電荷のような単一の磁極は存在しない」ことを示しています。N極から出た磁束は必ず S極に戻り、N極から出る磁束と S極に戻ってくる磁束の数は等しくなります。出るものと戻るものが等しいのですから、差し引きゼロなのです。

∇ と磁束密度の内積は発散 を表しますが、磁束密度が空間内で変化 (左辺) しても、そこからは何も湧き出さない (右辺) ということです。

電流が流れるとその周囲に磁束密度が生じます。磁束密度は電流のまわりを回転しています。このような回転しているようすを渦場と呼びます。対して、電荷から電束が出ていくようなようすは発散場と呼びます。
渦場の中に小さな小さな点のような体積を考えると、そこには磁束密度 (というベクトル) が入ってきてそのまま出ていく、つまり貫通していくだけです。発散場のような電界を湧き出すようなものはなにもありません。渦場の微小な体積から新たなベクトルは生まれませんから、磁束密度の発散はゼロなのです。

アンペール・マクスウェルの法則

「アンペール・マクスウェルの法則」です。

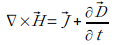
この式は「電流が流れると回転する磁界が生じる」ことを示しています。
磁束密度の発散はゼロだと学びました。じゃなにが磁界を産み出すのか？ アンペールの法則は「電流が流れると磁界が生じる」と示しています。マクスウェルの法則は「電界が変化すると変位電流が流れて磁界が生じる」といいます。その二つを合わせたのがこの式で、磁界を生じさせるものは伝導電流 (導体を流れる電流) と変位電流 (電界の変化で流れる電流) である、ということです。

は ∇ と磁界の外積をとるということで、磁界の回転 (rotation) を表します。 とも表現します。左辺を計算してみましょう。

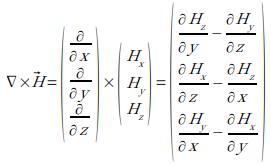
さて、恐ろしい式になってます (；´Д｀) が、∇ (ベクトル) と磁界 (ベクトル) の外積はベクトルで、その x 成分が、

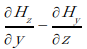
だということがわかります。そしてこれは「yz 平面から x 方向へ伸びるベクトルの回転量」を示している。y 成分、z 成分についても同様に、zx 平面から y 方向へ伸びるベクトルの回転量、xy 平面から z 方向へ伸びるベクトルの回転量です。回転方向は右向きです。それぞれは極小面積の回転ですが、全体 (単位面積) を合わせてみるとひとつの回転 (渦) になっている、と。
左辺は「磁界が渦を巻いている」ことを示しているとわかりました。

右辺です。
第1項の伝導電流密度 とは、導体に流れる単位面積あたりの電流です。電流とは単位時間 (1秒) に流れる電荷の量です。
第2項 は変位電流 [A/m²] を表します。たとえばコンデンサには交流電流が流れますが、そのとき電極間の電束密度は時間によって変化していきます。それを式で表したのが第2項。時間あたりの電束密度の変化量は、すなわち電流密度を表します。

ということで、この式は「伝導電流や変位電流が流れる (右辺) と回転する磁界が生じる (左辺)」ことを示しています。そして、その回転方向は電流の方向に対して右回転になります。

ファラデーの電磁誘導の法則

最後は「ファラデーの電磁誘導の法則」です。

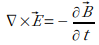
この式は「磁束密度が時間変化すると、まわりに電界が生じる」ことを示しています。マイナス符号は磁束密度の変化と反対方向に電界が回転することを示し、磁束密度が増加すると左向き、減少すると右向きに回転します。電界が生じると電荷が動き、電流となります。

は ∇ と電界の外積をとるということで、左辺は電界の回転 (rotation) を表します。 とも表現します。

右辺は、時間によって磁束密度が変化していることを表します。
磁束が変化すると、その変化を妨げるような方向の電流が流れる。電磁誘導とか、習いましたね。電流が流れるとは電荷が移動するということで、電荷が移動するのは電界から力を受けるから。つまり、磁束が変化すると電界が生じる、その方向は磁束の変化を妨げるような逆向きの磁束を生じさせる向きだ、ということです。

後記

今回は「マクスウェルの方程式」をちょっと噛ってみました。いろいろ書き散らしてきましたけど、冒頭にも書いたように理論的でも数学的でもない俺的備忘録です。

それぞれの式が示していること、どれも知ってます。電荷から電束が出るとか、磁極は N極と S極が対になっているとか、電流が流れると右向きに磁束ができること、磁束が変化すると逆向きの電流が流れることも。
でも、それを「方程式」にするとこうなるんだと知ったことが、今回の収穫です。これはクーロンやアンペールやガウスやファラデーやサバールやレンツや、そういういろいろな法則を数学的にまとめた方程式なのだから、それでいいのかも、などとも思うのです。

これから無線に関することもいろいろ勉強してみたいなと思っているのですが、そのなかで、いつか役に立つことがあったらいいな、と。