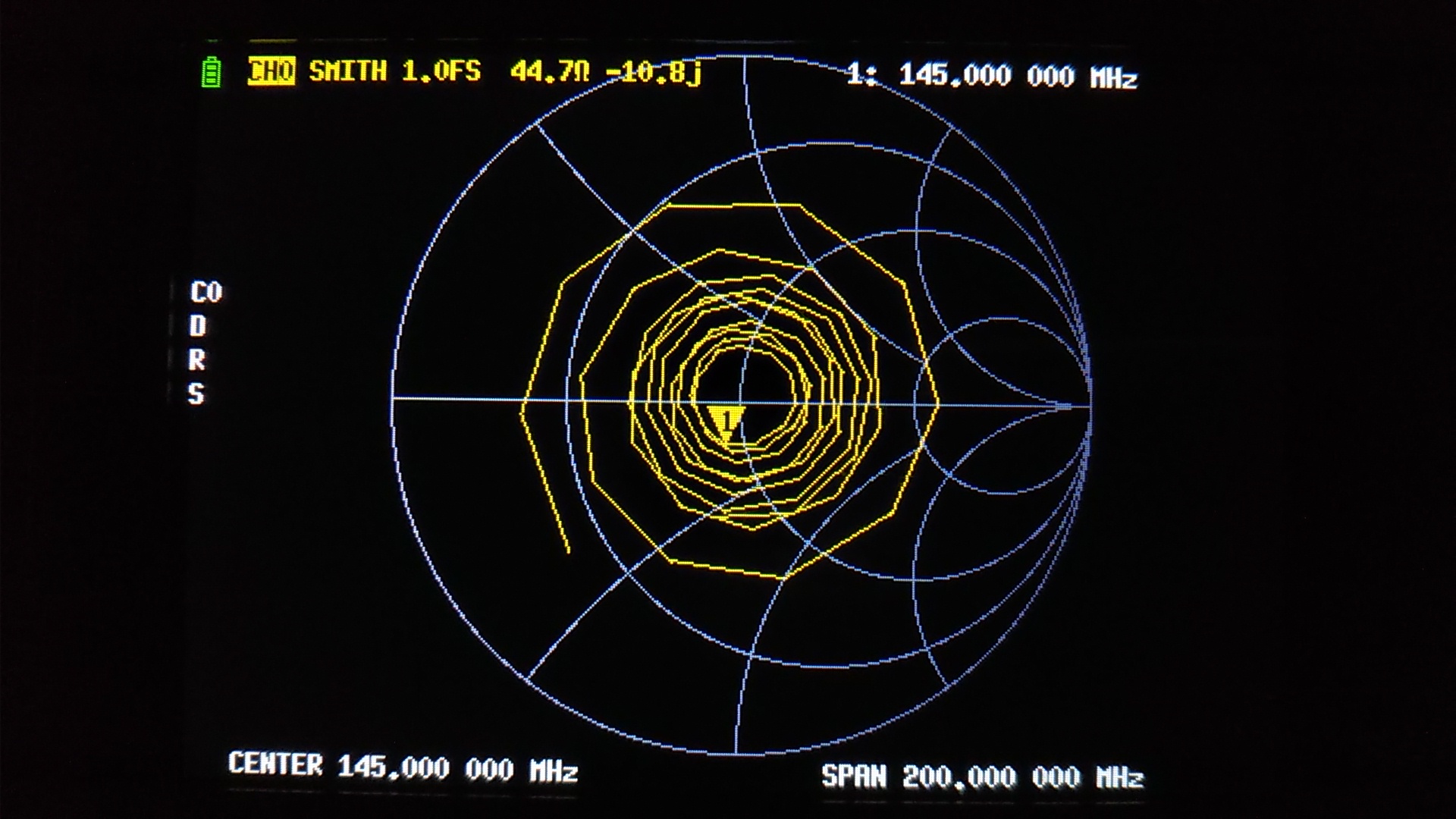
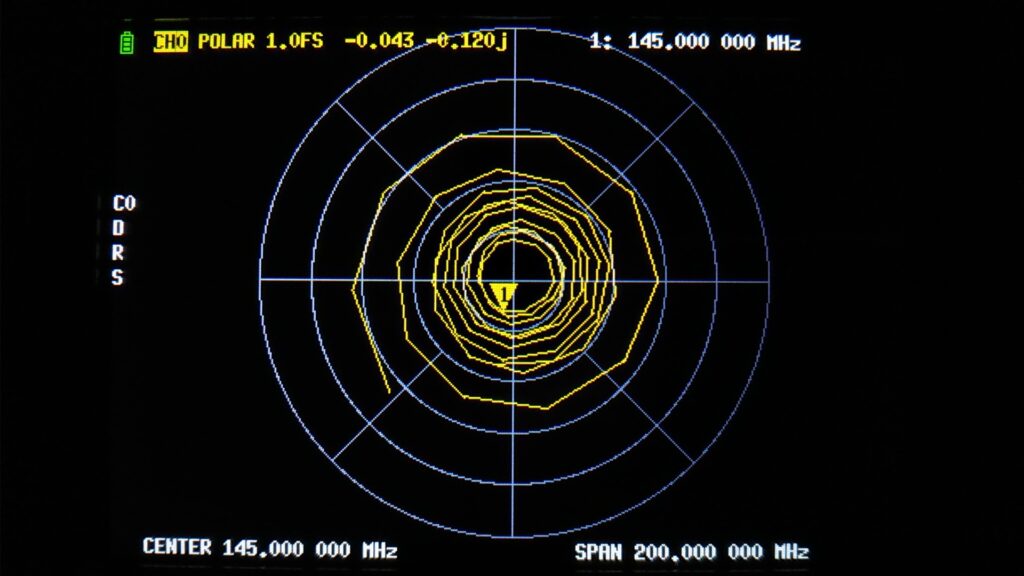
いきなりですが、ダミーアンテナに 5mほどの同軸ケーブルをつないで、送信機側から NanoVNAで測定、スミスチャートを表示してみました。
周波数軌跡がグルグルと 10回転。まるでクモの巣のようです。なんですか? これは。
今回は、この測定結果について考えます。
測定に使ったダミーアンテナについては、前回の記事を参照ください。
同軸ケーブルの長さを測る
まず、NanoVNA で同軸ケーブルの長さを計測しておきましょう。
NanoVNA は周波数領域解析を行ないます。入射波と反射波の振幅と位相を測定して、周波数に関するグラフを表示するってこと。で、NanoVNA は時間領域解析 (TDR : Time Domain Reflectmetry) もシミュレーションできて、時間に関するグラフも表示できます。まぁ要するに、グラフの横軸を周波数から時間に換えることができるってことかな。
なので、アンテナを外して開放した同軸ケーブルにステップ信号を送り、反射波が戻ってくるまでの時間を測定することで、同軸ケーブルの長さがわかります。
同軸ケーブル長の計測手順
- 測定周波数範囲 STIMULUS/START を 50K、STIMULUS/STOP を 400M に設定(*1)
- キャリブレーションを行なう
- 表示形式 DISPLAY/FORMAT/>MORE/REAL に設定
- TRANSFORM/LOW PASS IMPULSE を ON (文字反転) にする
- TRANSFORM/VELOCITY FACTOR に同軸ケーブルの短縮率 (%) を入力(*2)
- アンテナ側を開放した同軸ケーブルを CH0 に接続
- TRANSFORM/TRANSFORM ON を ON (文字反転) にする
- 反射波のピークの位置へ、マーカーを移動させる
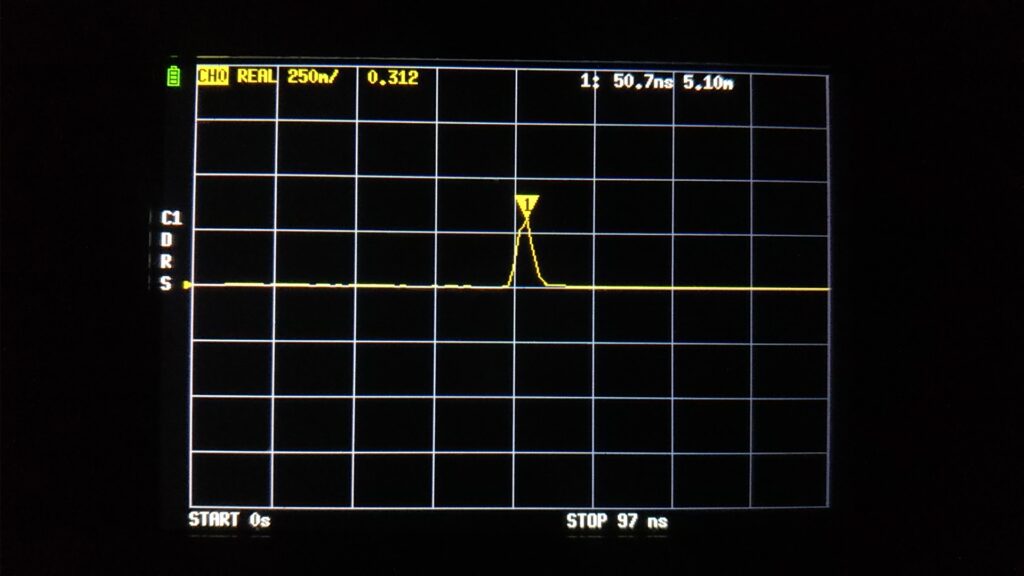
以上で、メインスクリーンの右上に「1: 50.7ns 5.10m」などと表示されます。50.7ns が信号が往復した時間、5.10m が同軸ケーブルの長さです。
(*2) 同軸ケーブルの短縮率はメーカー規格表による。RG58A/U の場合 0.67 (67%)
図2 に示すように、NanoVNA による同軸ケーブルの長さの計測結果は 5.10m でした。
実測値は 5.0m なんですけど、まぁどちらも精度がわからないのでなんとも言えませんね。NanoVNA が 5.10m と認識しているのですから、測定ではそうしておくほうがよさそうです。
ちなみに、アンテナ側を短絡した場合、反射波はマイナス側へ振れますが、同様に測定できます。
ということで、同軸ケーブルの物理長 L は 5.10m とします。また、使用している RG58A/U の短縮率は 0.67 ですので、ケーブル内の伝送速度 vg は、光の速度 v を 3×108 [m/s] として
vg = 3 x 108 x 0.67 = 2.01 x 108 [m/s]
となります。
送信機側からみた反射係数
昔から、アンテナの VSWR はアンテナ直下で測らないといけない、といわれています。送信機側で測ると異なった値になる。でも λ/2 長の同軸ケーブルをつなげば正しい値になる。などなど。
同軸ケーブルの長さは、反射係数に影響を与えるようです。
距離が変化するとき
負荷から離れた位置から測定したとき、反射係数がどうなるのかを調べてみましょう。
負荷 (アンテナ) から送信機側へどれだけか離れた位置から反射係数を測定すると、反射波の位相が変化するため、反射係数の絶対値を半径とする円を時計方向に描きます。そして、λ/4 だけ離れたとき半回転し、λ/2 まで離れると 1回転して元の位置にもどります。さらに離れていくと、この円上を時計方向に回転していきます。
どうしてそうなるのか。理論的なことは教科書などを参照してくださいませ。
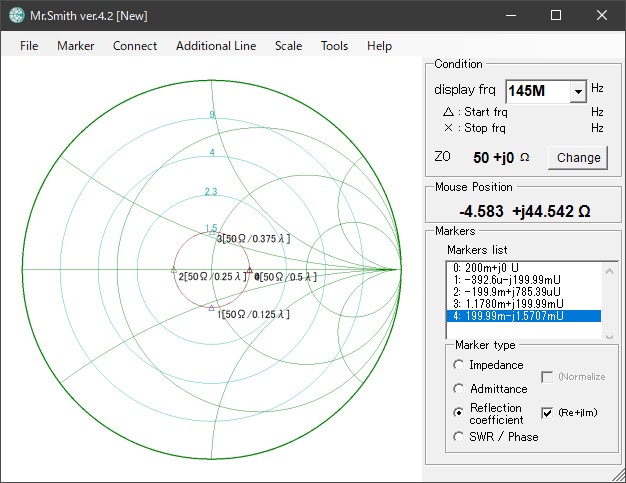
距離と反射係数の関係を、スミスチャート (反射係数面) で確かめたのが図3 です。
75Ωの負荷に 50Ωの同軸ケーブルをつなぐと反射係数は +0.2 です (Marker0)。負荷から λ/8 離れると反射係数は -j0.2 (Marker1) となり、λ/4 で -0.2 (Marker2)、3λ/8 で +j0.2 (Marker3) となって、λ/2 離れると元の位置に戻ります (Marker4)。
なお、Mr.Smith のスケールは VSWR 表示ですので、反射係数 0.2 は VSWR 1.5 です。チャートの外周で反射係数は 1.0、VSWR は ∞ になります。
周波数が変化するとき
NanoVNA での測定は周波数を変化させて行ないます。周波数が変化したときの反射係数を調べてみましょう。
同軸ケーブル内の伝送速度を 2.01×108m/s とすると、周波数が 45MHz の波長は 4.47m、145MHz で 1.39m、245MHz で 0.82m です。同軸ケーブルの長さを 5.10m とするとそれぞれ 1.14λ、3.68λ、6.22λ に相当し、周波数が高くなるにしたがって負荷からの距離が長くなっていく、ということになります。
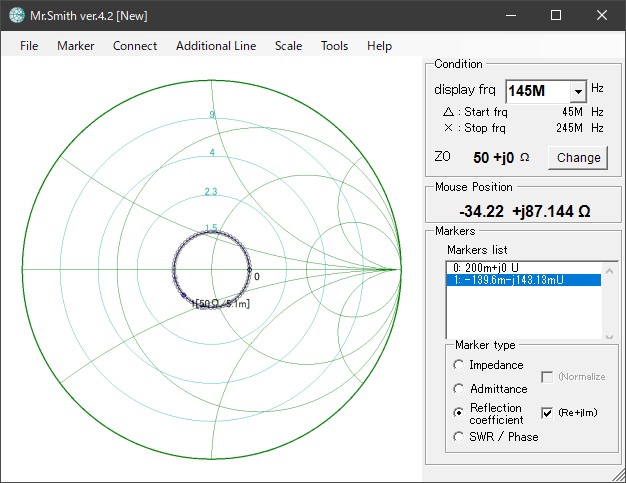
図4 は、周波数を変化させたときの反射係数を示した反射係数面です。
75Ω の負荷に 5.10m の同軸ケーブル (50Ω) を接続し、周波数を 45MHz~245MHz に変化させました。反射係数は図3 と同じように、半径 0.2 の円上を時計回りに回転していきます。
また、周波数が 145MHz のときの反射係数は -0.140-j0.143 と読みとれます。
RLC直列回路をつなぐ
では、負荷として RLC直列回路をつなぐとどうなるでしょうか。
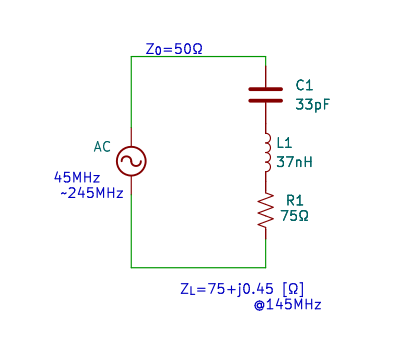
図5 は、ダミーアンテナを作ったときの RLC直列回路です。この回路に伝送路として 5.10m の同軸ケーブルをつないだ場合を考えます。
なお、同軸ケーブルの短縮率 k は 0.67 ですので、比誘電率 ε を
k = 1 / √ε ε = 1 / k2 = 1 / 0.672 = 2.228
として、Mr.Smith に設定しました。
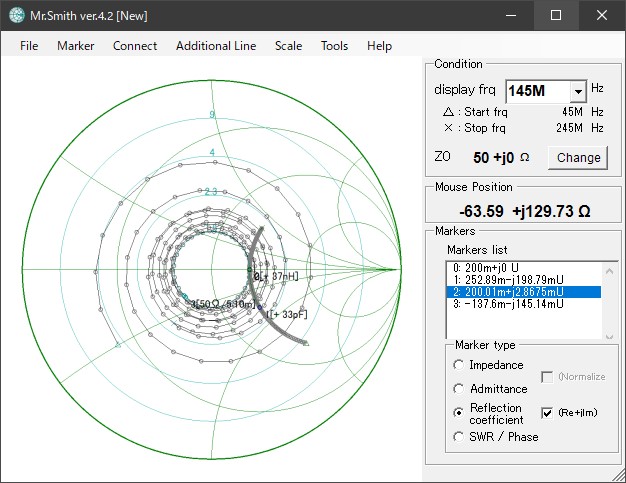
図6 がこのときの反射係数面です。周波数の上昇に伴い、反射係数がグルグルと回転しています。
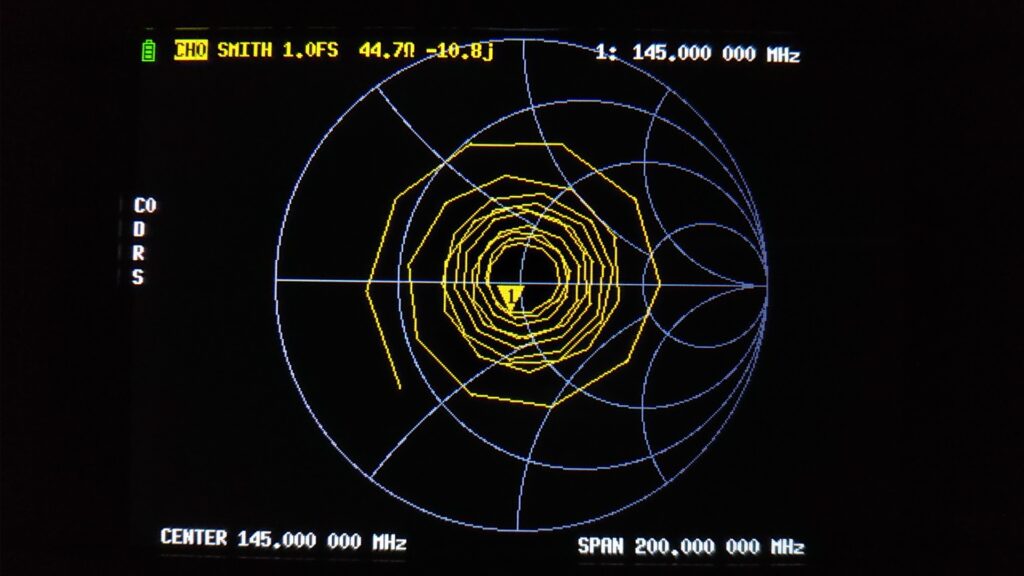
図7 に、冒頭の図1 を反射係数面に表示した測定結果を示します。ダミーアンテナに 5m ほどの同軸ケーブルをつないで送信機側から NanoVNA で測定してみた結果は、RLC直列回路を離れた位置から測定した結果に相違ないようです。
周波数 145MHz での反射係数は、Mr.Smith では -0.138-j0.145 です。75Ωの負荷をつないだ場合とほぼ一致しています。
また NanoVNA での測定値は -0.043-j0.12 でした。数値はやや違いますが、どちらも第3象限の近い位置にあります。
この反射係数をインピーダンスにすると 36.5-j11.0Ω です。ダミーアンテナのインピーダンスは 74.4+j0.0424Ω ですので、かなり異なった値になっています。同軸ケーブルがインピーダンスを変化させていることがわかります。
反射係数 Γ=-0.043-j0.12 とすると、VSWR は、
|Γ| = √(0.0432 + 0.122) = 0.127
VSWR = (1 + |Γ|) / (1 - |Γ|) = ( 1 + 0.127) / (1 - 0.127) = 1.29
アンテナ直下の VSWR は 1.5 ですので、送信機側で VSWR を測定すると値が改善してみえることになります。
ダミーアンテナを測定する
では、もう一度ダミーアンテナを測定してみましょう。今度は、測定周波数範囲を CENTER 145MHz、SPAN 10MHz とし、キャリブレーションを行ないました。
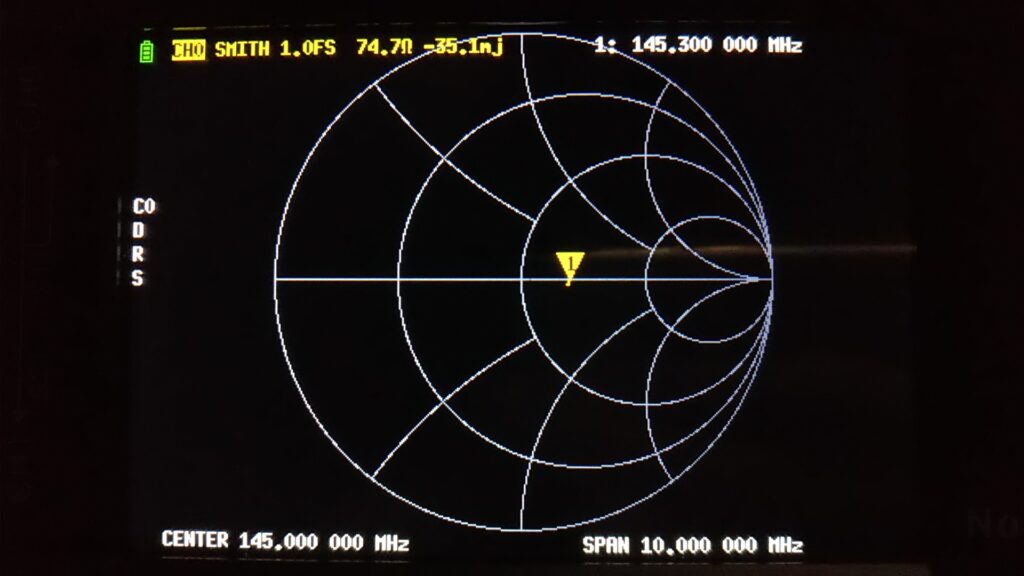
図8 が、ダミーアンテナを直下で測定したスミスチャートです。
最もリアクタンスが小さくなる周波数は 145.3MHz です。ここがアンテナの共振周波数です。共振点でのインピーダンスは 74.7-j0.0351Ω、反射係数は 0.198-j0.000 でした。
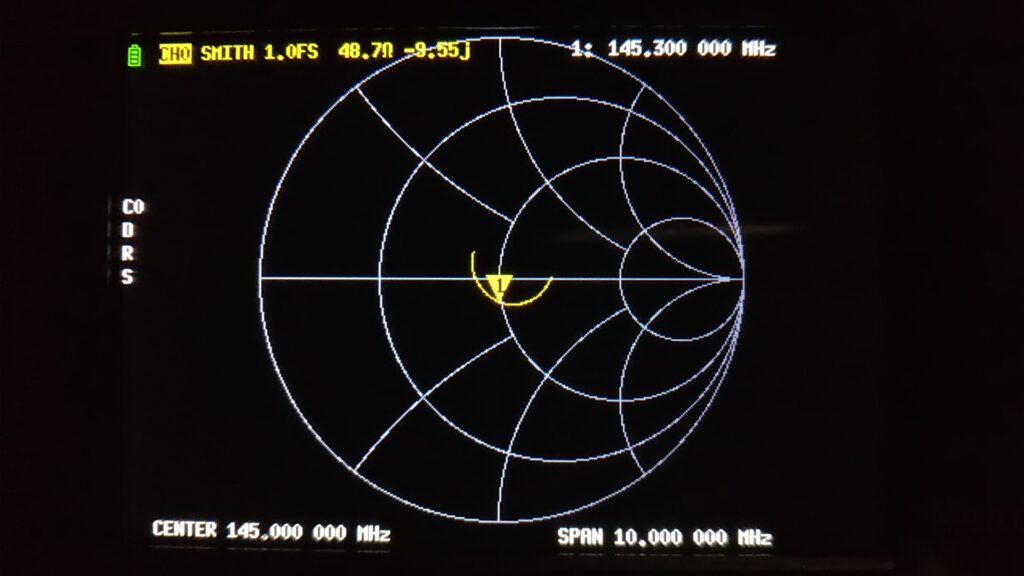
図9 は、送信機側でダミーアンテナを測定したスミスチャートです。同軸ケーブルの長さは 5.10m で、共振周波数 145.3MHz では 3.69λ に相当します。
送信機側で測定したインピーダンスは 48.7-j9.55Ω、反射係数は -0.003-j0.096 でした。
図らずも送信機とマッチングしちゃってますが、騙されてはいけませんよ。
ちなみに、送信機側の測定値から逆算してダミーアンテナのインピーダンスを求められないかなぁと思ってやってみたんですけど、そうは問屋が卸さない。たぶん、同軸ケーブルの損失とかいろいろあるから、簡単にはいかないですね。でもまぁ、軌跡からだいたいの見当はつけられそうですけど。
後記
今回は、ダミーアンテナを NanoVNA で測定してみました。やっぱりアンテナの測定は、アンテナ直下で行わないといけないようですが、昔と違って、なにかうまい方法あるんじゃないでしょうか? ねぇ?
さて、相変わらず難しいことはわかりませんが、NanoVNA の使い方の一歩目ぐらいは進めたかな。なので次は、ダイポールアンテナの調整をやってみようと思います。