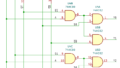
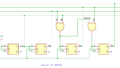
JKフリップフロップを使ったカウンタ回路をつくってみました。
11進~16進同期カウンタは、続きの記事を参照ください。
Dフリップフロップを使ったカウンタ回路は下記を参照ください。
JKフリップフロップの動作
JKフリップフロップの動作をおさらいしておきましょう。
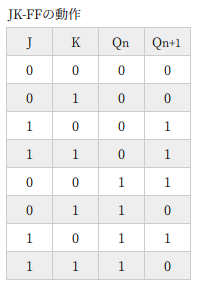
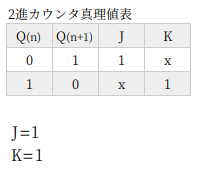
表1 は JKフリップフロップの真理値表です。
J、K は入力、Qn は現在の出力、Qn+1 は次の出力の状態です。
たとえば 3行目、入力 (J,K) が (1,0) で Qn=0 のとき、Qn+1 は 1 に変化します。入力が同じ (1,0) であっても、7行目のように Qn=1 のときは、Qn+1 は変化しません。
入力が (0,1) のときは、Qn=1 のとき Qn+1=0 へ変化しますが、Qn=0 のときは Qn+1 は変化しません。
また、入力が (0,0) のときは出力は変化しません。(1,1) のときは、出力がトグルする T フリップフロップの動作となります。
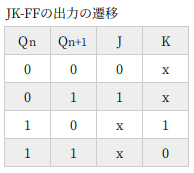
表2 は、JKフリップフロップの励起表です。
励起表とは、出力を Qn から Qn+1 へ遷移させるための入力を示す表です。俺はどちらも真理値表と書いてますが、まぁ気にしないでくださいまし。
出力が 0 → 1 に変化するのは J=1 のときで、K は don’t care (0 でも 1 でもかまわない) です。同様に、出力が 1 → 0 に変化するのは K=1 のときで、J は don’t care です。
JKフリップフロップは、Qn=0 のときは J によって、Qn=1 のときは K によって Qn+1 が変化する、ということがわかります。
2進~10進同期カウンタ
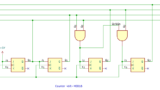
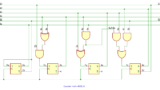
JKフリップフロップを使用した 2進~10進同期バイナリアップカウンタの回路例です。
フリップフロップとかカウンタとか真理値表とかカルノー図とか、基本的なことは教科書みるか、グーグル先生に尋ねてください。なお、シミュレーションは、verilogHDL によって論理式について行なっており、回路図と連動していません。回路はじっさいに製作しておらず、動作を確認していません。
2進カウンタ
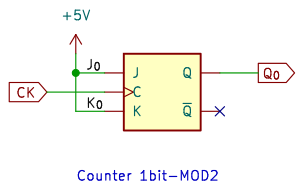
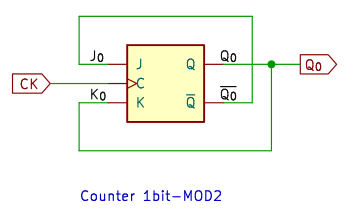
2進カウンタです。
クロックが入るたびに出力がトグルする Tフリップフロップになっています。J、K ともに 5V につなぐ回路 (左側) が一般的だと思いますが、don’t care を 0 とみなして、出力 Q を K に、反転出力 Q を J にもどす方法 (右側) もあります。
偶数の n進カウンタは LSB が 1 と 0 の交互になるので、初段は必ずこの回路になります。

3進カウンタ
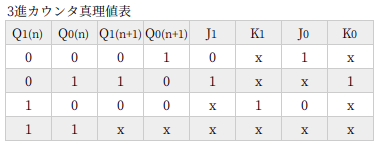
前出の表2 JKフリップフロップの励起表から、左の真理値表を埋めていきます。
Q(n)=0 → Q(n+1)=0 と変化しないとき J=0 です。Q(n)=0 → Q(n+1)=1 と変化するときは J=1 になります。
Q(n)=1 → Q(n+1)=0 となるときは K=1 です。

3進カウンタですので、(1,0) の次が (0,0) にもどります。
真理値表をみつめれば論理式は求められそうですが、考えているうちにできちゃうので、カルノー図を書きました。
論理式より組み立てた回路が下図。2ビットカウンタでは、まだゲート回路は不要です。
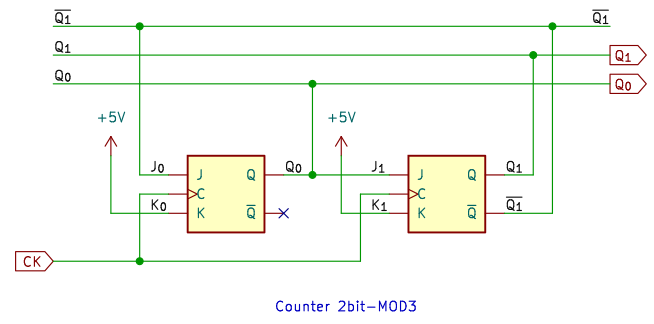
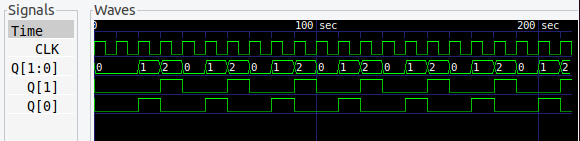
4進カウンタ
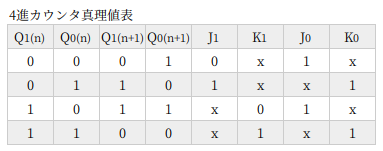
4進カウンタは基本的なカウンタ回路で、これも真理値表をみつめれば論理式が求められそうです。

が、念のためにカルノー図を書いておきました。
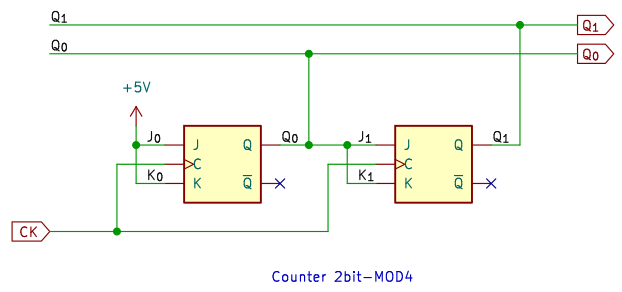
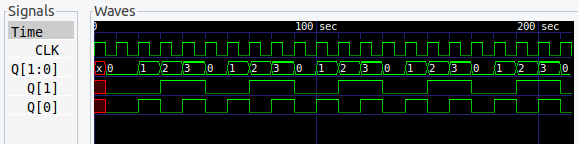
5進カウンタ
5進カウンタから 3ビットになり、JKフリップフロップが 1つ増えます。
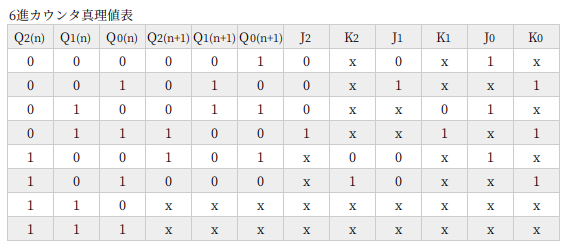
真理値表も大きくなってくるのでちょっとわかりにくくなりますが、Q(n) → Q(n+1) の遷移にたいして J、K の状態が決まることに注目すれば理解できると思います。
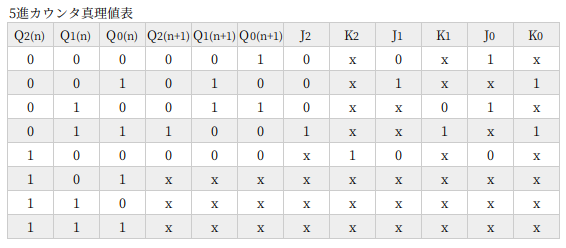
カルノー図は Q(n) をみて書きます。JKフリップフロップを使ったカウンタ回路では、カルノー図はわりと簡単になります。つまり、ゲート回路も簡単になるってことですね。
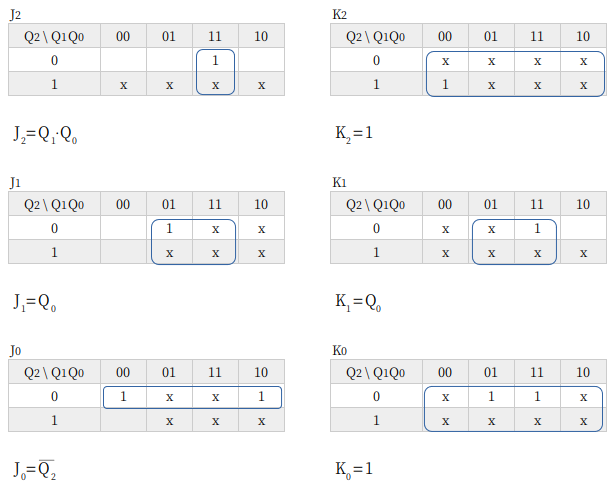
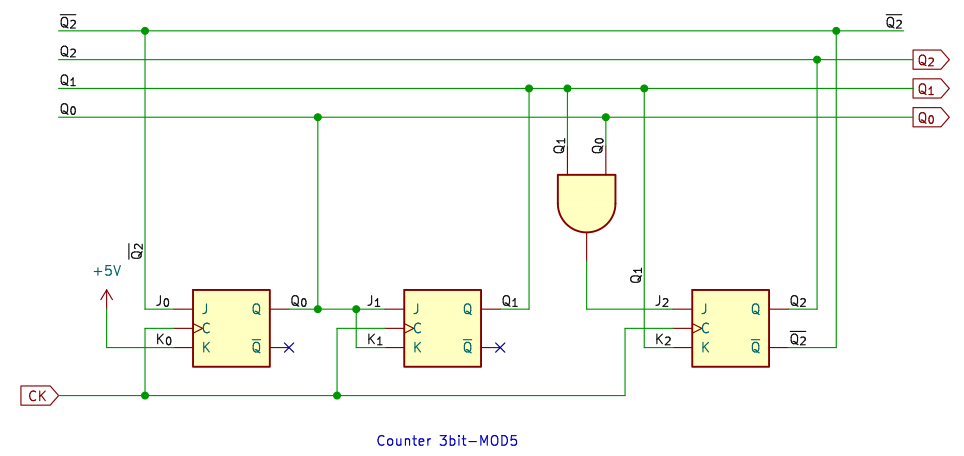
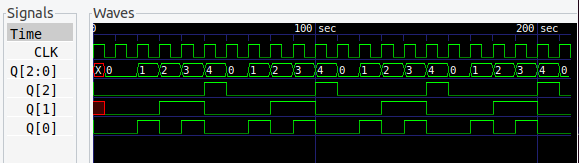
6進カウンタ
6進カウンタも、かわったところはありません。同様につくっていくだけです。
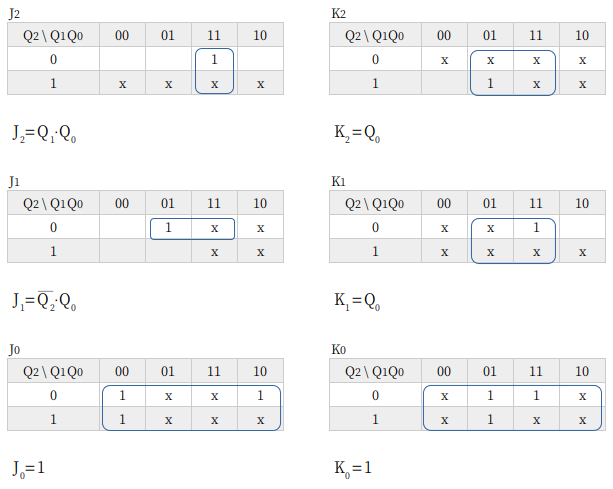
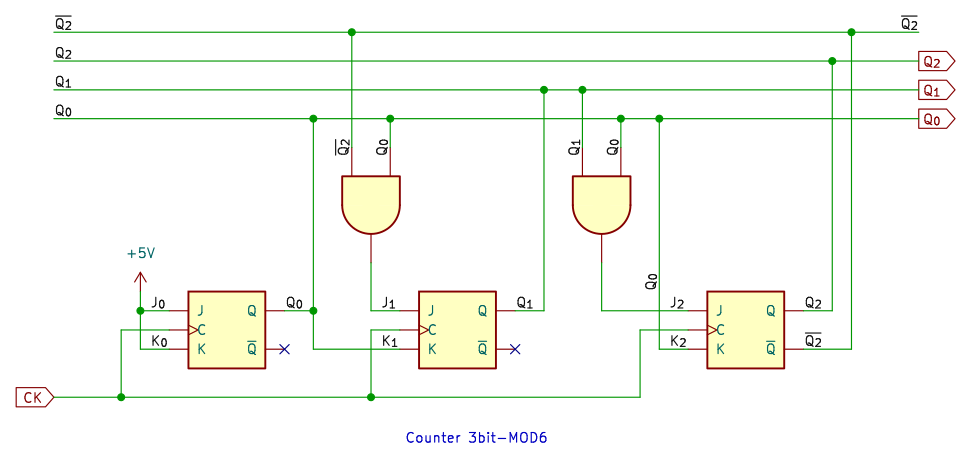
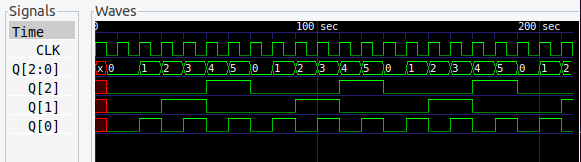
7進カウンタ
7進カウンタもかわりないですが、論理式に OR がでてきました。
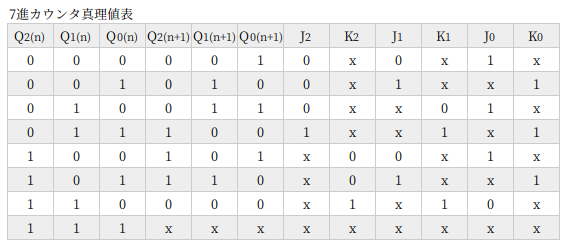
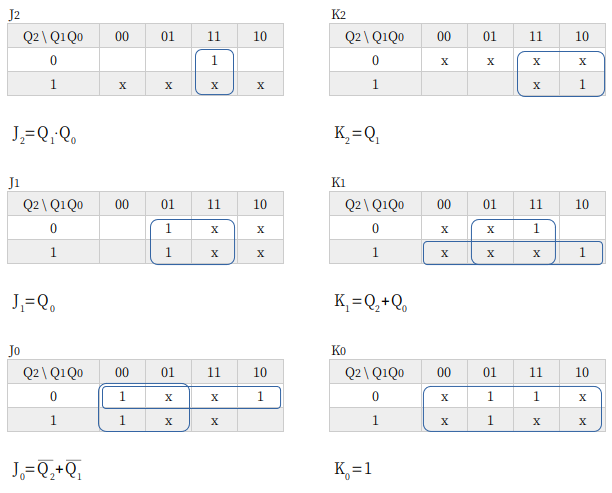
たとえば J0=Q2+Q1 ですが、ド・モルガン変換すると J0=Q2⋅Q1 になります。つまり、OR ではなくて NAND を使えば、反転出力を使わない回路ができます。じっさいに回路を組むとき、どのゲートIC を使うかによってどちらを選ぶか決めますが、ここでは AND と OR に統一することにしました。
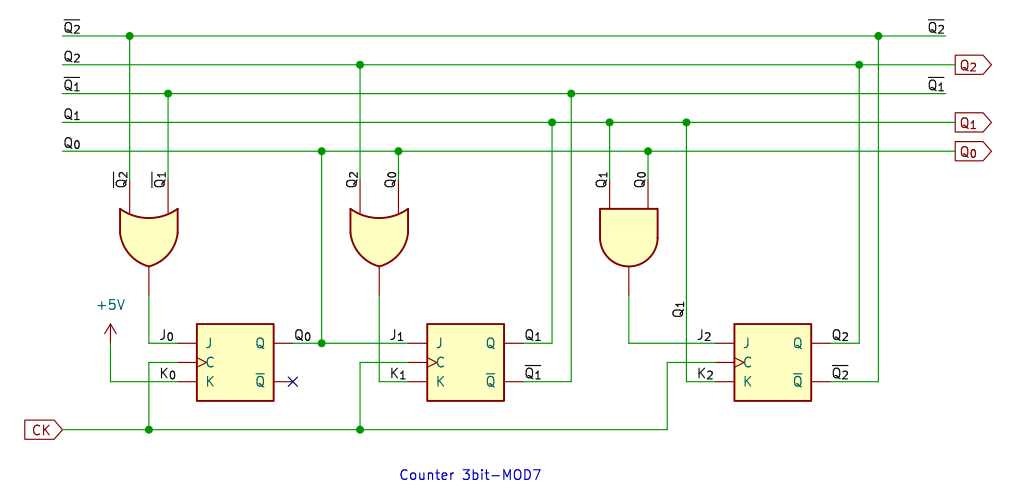
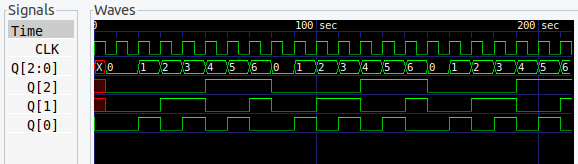
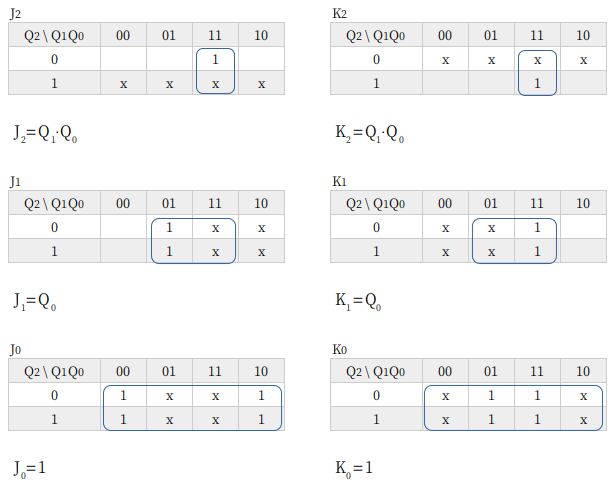
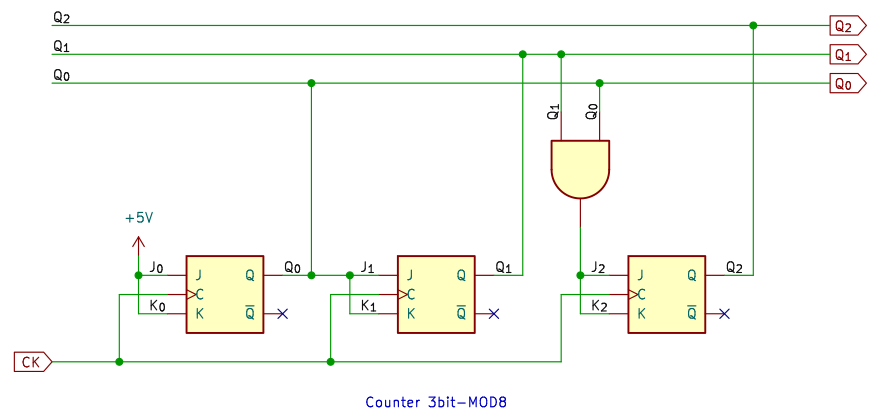
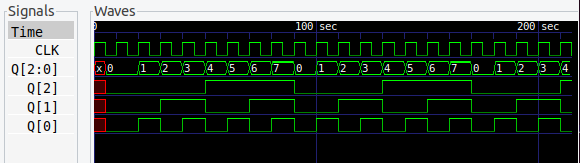
8進カウンタ
8進カウンタは 4進や 16進と同様に (2n)進カウンタで、これも基本的な回路です。
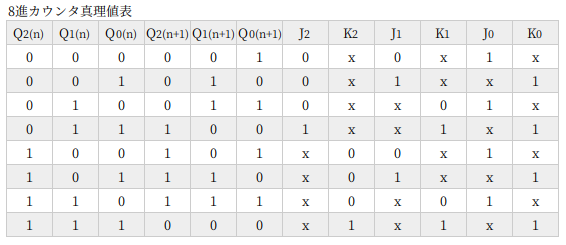
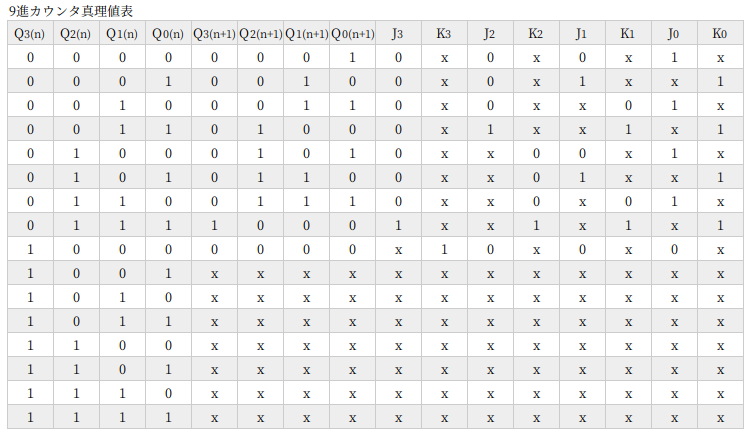
9進カウンタ
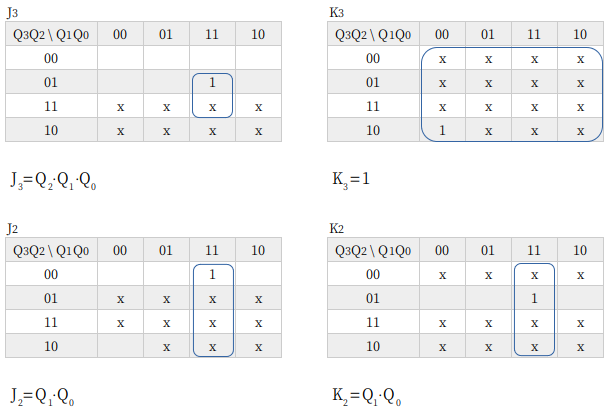
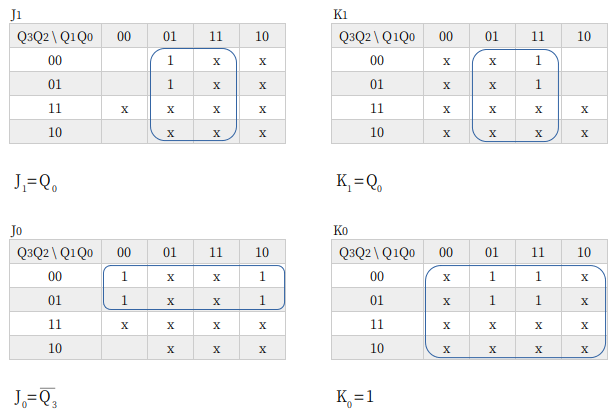
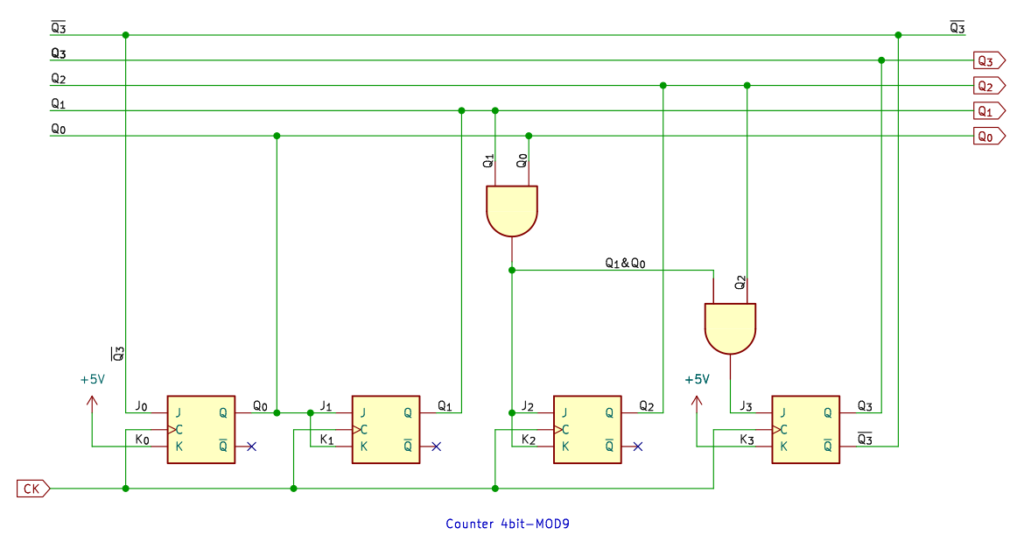
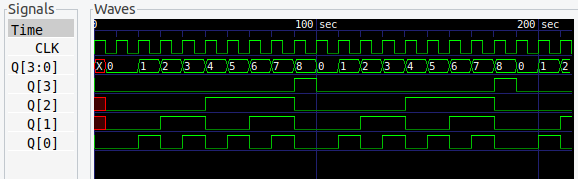
9進カウンタから 4ビットになり、さらに JKフリップフロップが増えます。真理値表もさらに大きくなりますが、基本はこれまでと同じです。
カルノー図は don’t care が多いので、あまり難しくならないんですよね。
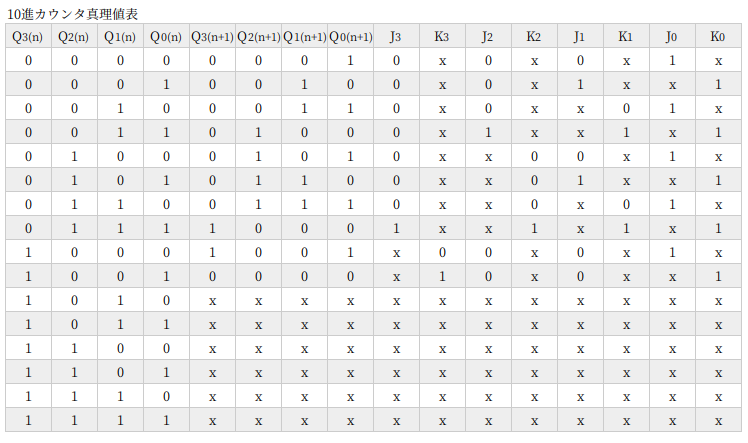
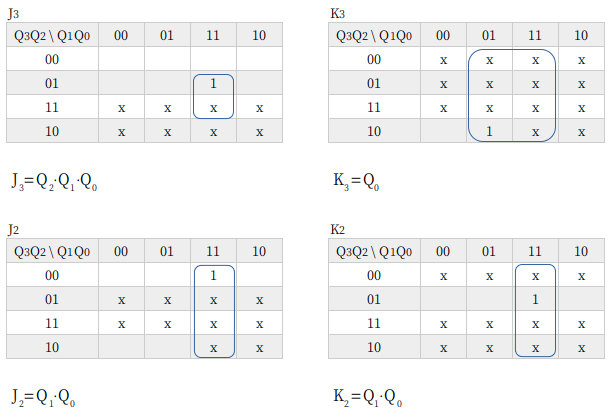
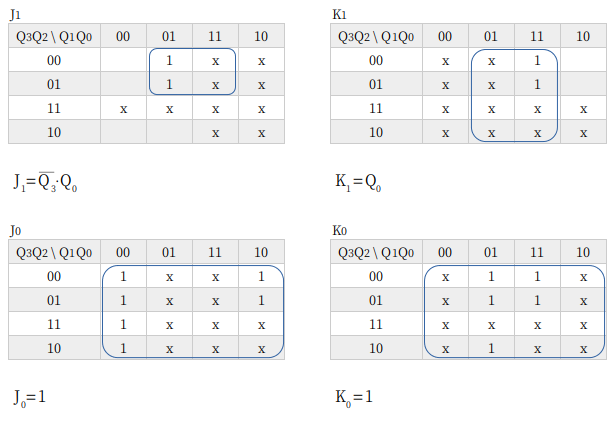
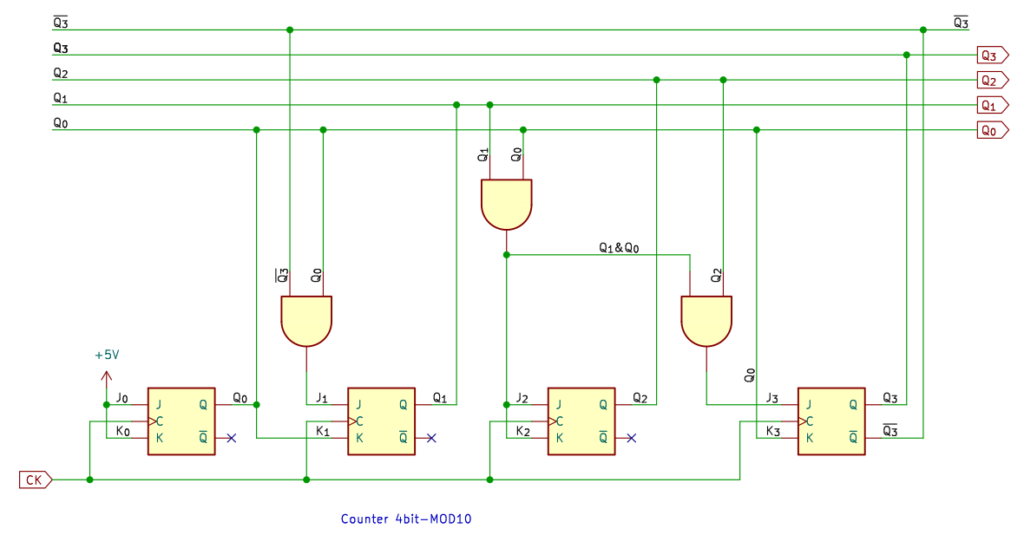
10進カウンタ
10進カウンタは、BCDを出力するためによく使われるカウンタです。10進数を扱うにはかかせません。
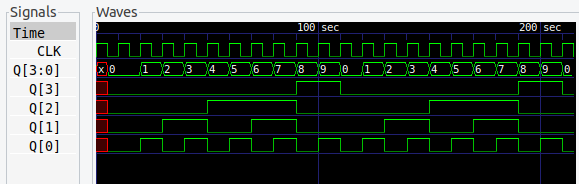
後記
ここまで、JKフリップフロップを使った 2進~10進カウンタ回路をつくってきました。
以前つくった Dフリップフロップを使ったカウンタ回路 (参考記事) と比較してみると、JKフリップフロップを使ったカウンタ回路のほうがゲート回路がとても簡単です。そのせいか、カウンタ回路をググると JKフリップフロップを使った回路が多くみられるようです。
でも、真理値表をみるとちょっと複雑なんですよね。わかってしまえばどうということはないのですが、頭痛くなっちゃう。どちらを選ぶかは、お好みで。
では、次は 11進~16進カウンタをつくっていきましょう。だんだん複雑になっていきますが、基本はすべて同じです。