デジタル時計をつくったりして時間があいてしまいましたが、論理回路の勉強を続けましょう。
今回は、シフトレジスタと、それを応用したカウンタを試してみます。
シフトレジスタ
シフトレジスタとは、複数のフリップフロップがカスケード接続された構造で、クロックパルスが入力されるたびに、記憶されているデータが次のフリップフロップへ移動していく論理回路です。
詳しくは、ググってください m(_ _;)m
フリップフロップの伝送遅延時間
シフトレジスタの動作を理解するうえでのポイントは、クロックが入ってからフリップフロップの出力が変化するのに、伝送遅延時間があるってこと。
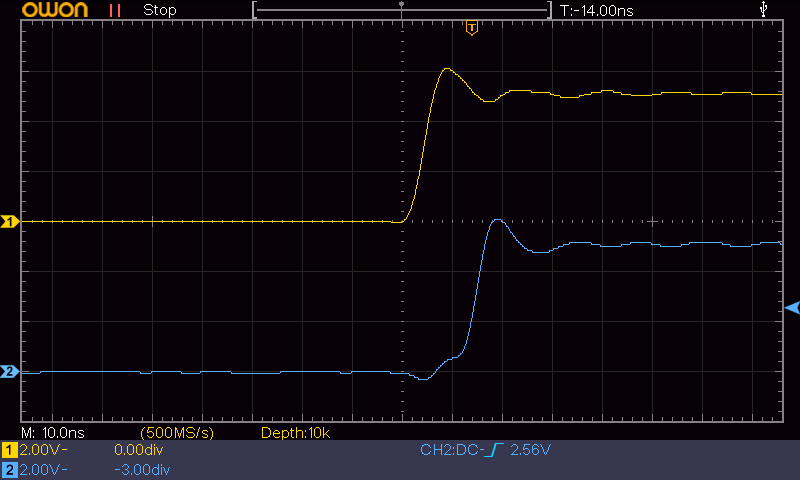
図1 は、実験に使った Dフリップフロップ 74HC74A の、クロック (黄) と出力 (青) の立ち上がり部の波形です。クロックが入って、10nsほど遅れて出力がでていることがわかります。
クロックより遅れて出力が立ち上がるから、次段のフリップフロップの出力は次のクロックの立ち上がりで動作する。そうしてフリップフロップは、クロックひとつづつ遅れて順番に動いていき、データが移動していくようになる。ということ。
ちなみに、74HC74A のデータシートでは、伝送遅延時間は 16ns (Vcc=4.5V、標準) になっていました。最小値の規定がないのですが、まぁだいたいこのぐらいってことなのだろうと思います。
周辺回路
まず、実験に必要な周辺の回路をつくっておきましょう。
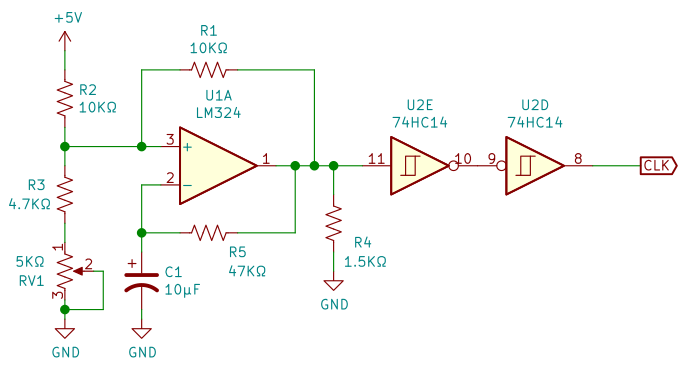
図2 は、クロック発振回路です。
なんでもいいんですけど、前回の記事でつくったオペアンプを使った矩形波発振回路がありましたので、それを使っています。
どうせ 74HC14 使うので、こっちとかが簡単でおすすめです。
発振周波数は約 2Hz。ボリューム RV1 は、出力パルスのデューティ比の調整用で、デューティ比 50%に調整しておきます。
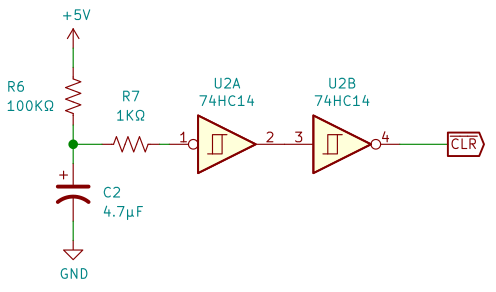
図3。毎度毎度の、電源オン時にフリップフロップを初期化する回路です。
フリップフロップは、電源オン時に出力が不定になりますので、CLR を LOW にして、出力を初期化しておきます。
電源オン後 500msで HIGH が出力されます。
R7 は ICの保護抵抗です。
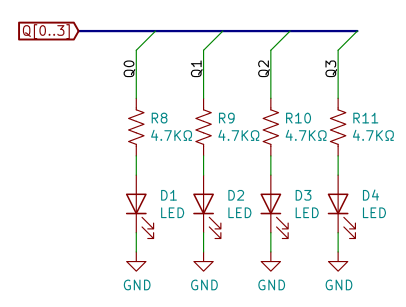
図4 は、フリップフロップの各段の出力を LED 表示するための回路です。
LED の表示によって、シフトレジスタの動きがわかると思います。
LED電流は約 0.6mA。ふつうの高輝度 LEDなら、この程度の電流でもじゅうぶんに光ります。
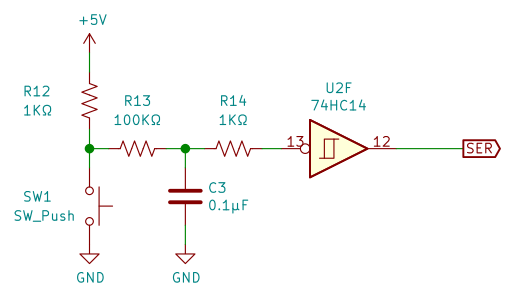
図5 は、入力信号を与えるための押しボタン回路です。
R13、C3のフィルタ回路でチャタリングを抑止し、シュミットトリガで波形整形します。
R12 はプルアップ、R14は保護抵抗です。
シフトレジスタの回路
シフトレジスタには、入力がシリアルのものとパラレルのものがあります。また、出力もシリアル、パラレル両方があります。今回はそのうち、シリアル入力パラレル出力 (Serial-In, Parallel-Out, SIPO) で、フリップフロップが 4段の 4ビットシフトレジスタをつくってみました。
74HCシリーズだと 74HC164 が相当しますが、74HC164 はフリップフロップが 8つ接続されている 8ビットシフトレジスタですので、その半分の規模です。
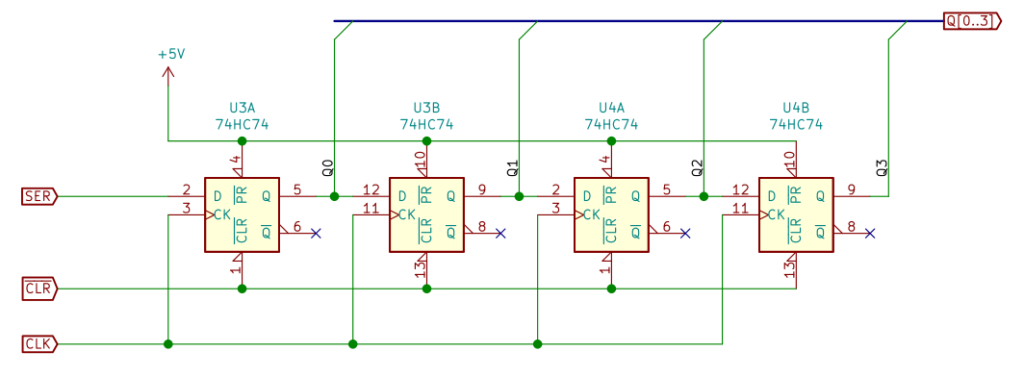
使ったのは、Dフリップフロップの 74HC74A です。ググるとよくでてくる回路ですね。
出力 Q0~Q3 の初期値は 0 です。押しボタンを押下して SER が 1 になると、最初のクロックの立ち上がりで Q0 が 1、次のクロックで Q1 が 1 になり、クロックが入るたびに次段に送られていきます。SER が 0 になると、それも順番に次段に移動していきます。
verilogHDL によるシミュレーション
オシロスコープでは全体の信号の動きが見られないので、verilogHDL でシミュレーションしてみました。
- module TC74HC74A (
- input wire D, CK, PR, CLR,
- output reg Q, NQ
- );
- always @(posedge CK, negedge PR, negedge CLR) begin
- if(1'b0 == CLR) begin
- if(1'b0 == PR) begin
- Q <= 1'b1;
- NQ <= 1'b1;
- end
- else begin
- Q <= 1'b0;
- NQ <= 1'b1;
- end
- end
- else if(1'b0 == PR) begin
- Q <= 1'b1;
- NQ <= 1'b0;
- end
- else begin
- Q <= D;
- NQ <= ~D;
- end
- end
- endmodule // TC74HC74A
- module ShiftRegister (
- input wire CLK, CLR, SER,
- output wire [3:0] Q,
- output wire [3:0] NQ
- );
- TC74HC74A ff0(.D(SER), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[0]), .NQ(NQ[0]));
- TC74HC74A ff1(.D(Q[0]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[1]), .NQ(NQ[1]));
- TC74HC74A ff2(.D(Q[1]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[2]), .NQ(NQ[2]));
- TC74HC74A ff3(.D(Q[2]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[3]), .NQ(NQ[3]));
- endmodule // ShiftRegister
回路記述は、一般的なシフトレジスタの記述ではなく、図6 の回路をそのまま記述しています。1~27行目が、使用した 74HC74A のモジュール。これを下位モジュールとして接続 (35~38行目) し、シフトレジスタ回路をつくっています。
シミュレーションの結果が、図7 です。
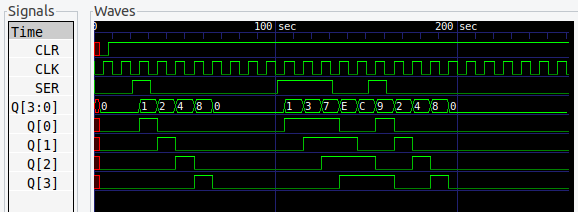
入力 SER が入ると、その信号が Q[0]~Q[3] へとシフトしていくようすがわかります。そして、Q[3] を通り過ぎた信号は、どこかへと消え去ってしまうのです (^_^;)
同じシフトレジスタでも、74HC595 は出力にストレージレジスタを持っていますので、各出力値を保持できるんですけどね。74HC164 では、データはどんどんシフトしていってしまいます。
ジョンソンカウンタ
シフトレジスタができましたので、それを応用したカウンタをつくってみましょう。まずはジョンソンカウンタと呼ばれる回路です。
ジョンソンカウンタ回路図
ジョンソンカウンタとは、ジョンソンさんがつくったカウンタです (^_^;)
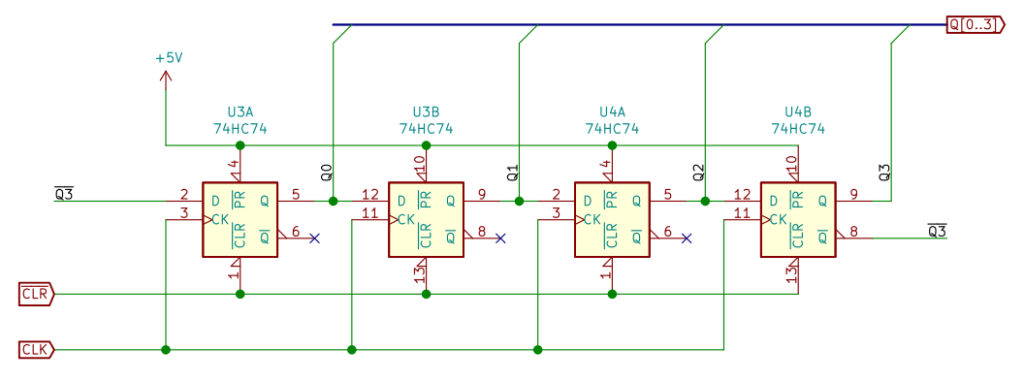
シフトレジスタと、どこが違う?
初段の信号入力が Q3 になっています。Q3 とは、最終段の出力を反転させた信号。ジョンソンカウンタとは、最終段の出力を反転させて初段の入力にもどし、ループにした回路です。
ジョンソンカウンタのシミュレーション (非対称型)
シミュレーションしてみましょう。
- module TC74HC74A (
- input wire D, CK, PR, CLR,
- output reg Q, NQ
- );
- always @(posedge CK, negedge PR, negedge CLR) begin
- if(1'b0 == CLR) begin
- if(1'b0 == PR) begin
- Q <= 1'b1;
- NQ <= 1'b1;
- end
- else begin
- Q <= 1'b0;
- NQ <= 1'b1;
- end
- end
- else if(1'b0 == PR) begin
- Q <= 1'b1;
- NQ <= 1'b0;
- end
- else begin
- Q <= D;
- NQ <= ~D;
- end
- end
- endmodule // 74HC74A
- module JohnsonCounter (
- input wire CLK, CLR,
- output wire [3:0] Q,
- output wire [3:0] NQ
- );
- TC74HC74A ff0(.D(NQ[3]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[0]), .NQ(NQ[0]));
- TC74HC74A ff1(.D(Q[0]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[1]), .NQ(NQ[1]));
- TC74HC74A ff2(.D(Q[1]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[2]), .NQ(NQ[2]));
- TC74HC74A ff3(.D(Q[2]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[3]), .NQ(NQ[3]));
- endmodule // JohnsonCounter
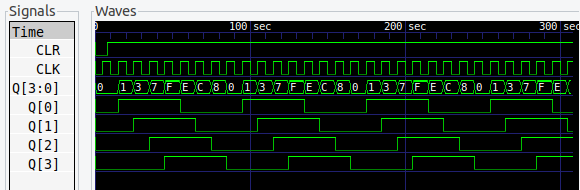
シフトレジスタと同様に、図8 の回路をそのまま記述しています。初段のインスタンス ff0 の入力は、最終段 ff3 の反転出力になっています。
| Q[3..0] | Q3 | Q2 | Q1 | Q0 |
| 0x0 | 0 | 0 | 0 | 0 |
| 0x1 | 0 | 0 | 0 | 1 |
| 0x3 | 0 | 0 | 1 | 1 |
| 0x7 | 0 | 1 | 1 | 1 |
| 0xF | 1 | 1 | 1 | 1 |
| 0xE | 1 | 1 | 1 | 0 |
| 0xC | 1 | 1 | 0 | 0 |
| 0x8 | 1 | 0 | 0 | 0 |
初期化後の Q3 は 1 です。それが初段の入力になるので、各出力は順次 1 になっていきます。最終段の出力 Q3 が 1 になると、Q3 は 0。それが初段にもどるので、今度は順次 0 になっていきます。最終段が 0 になると入力はまた 1 になる。それを繰り返します。
これは 8分周回路になっていることがわかります。ジョンソンカウンタは、段数 x2 の分周回路です。たとえば 3段目の出力をもどせば、6分周回路になります。8ビットの 74HC164 を利用すれば、最大 16分周することが可能です。
表1 は、ジョンソンカウンタの出力をビットコードにしたものです。
1 の数が増えていって、全部が 1 (0xF) になると、今度は減っていきます。このように、0 と 1 の期間が不均一のものを「非対称型」と呼びます。
ジョンソンカウンタのシミュレーション (対称型)
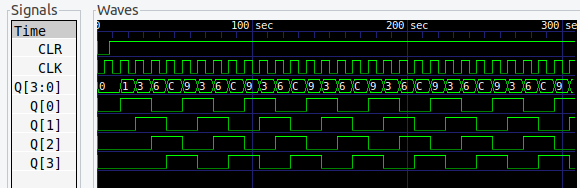
では、初段にもどす信号を 2段目の Q1 にするとどうなるでしょう。シミュレーションしてみます。
- TC74HC74A ff0(.D(NQ[1]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[0]), .NQ(NQ[0]));
| Q[3..0] | Q3 | Q2 | Q1 | Q0 |
| 0x3 | 0 | 0 | 1 | 1 |
| 0x6 | 0 | 1 | 1 | 0 |
| 0xC | 1 | 1 | 0 | 0 |
| 0x9 | 1 | 0 | 0 | 1 |
2段目の出力をもどしているので 4分周回路になりましたが、フリップフロップは 4段あるので、出力は 4ビットのままです。
表2 が、出力コードです。
すべての状態で、1 と 0 の数が同じになりました。これを「対称型」と呼びます。
ということは、Q3 をもどす非対称型でも、フリップフロップを 8段にすれば対称型になる。容易に想像できますね。
リングカウンタ
ジョンソンカウンタもリングカウンタの一種なのですが、最終段の出力を反転せずに、そのまま初段にもどすのがリングカウンタです。
ただ、初期化時にはすべての出力が 0 なので、最初だけ 1 を与えてやらないといけません。初期化時に初段を 1 にセットするという方法もありますが、ふつうは「最終段を除く出力がすべて 0 になったときに 1 をもどす」という方法をとります。
リングカウンタ回路図
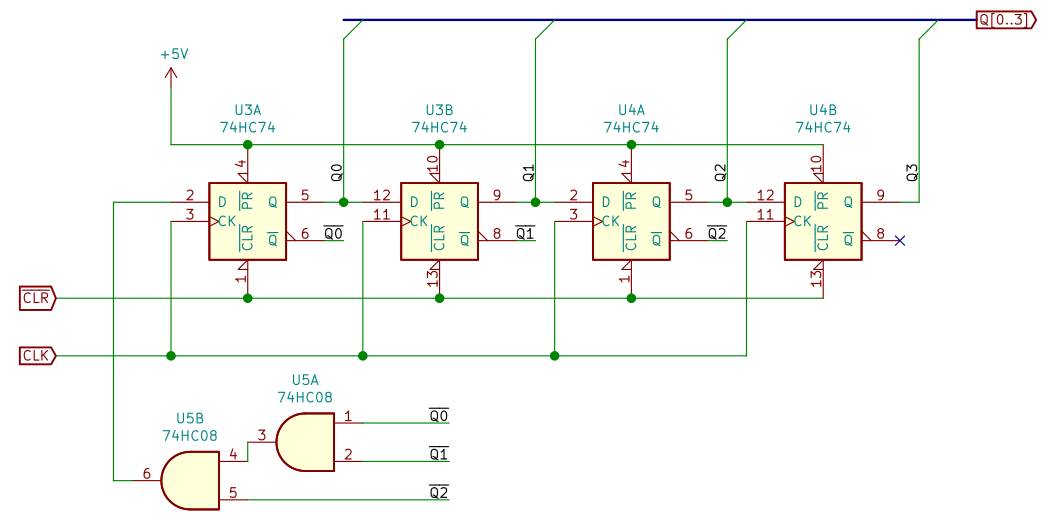
図11 が、「最終段を除く出力がすべて 0 のとき 1 をもどす」リングカウンタの回路です。
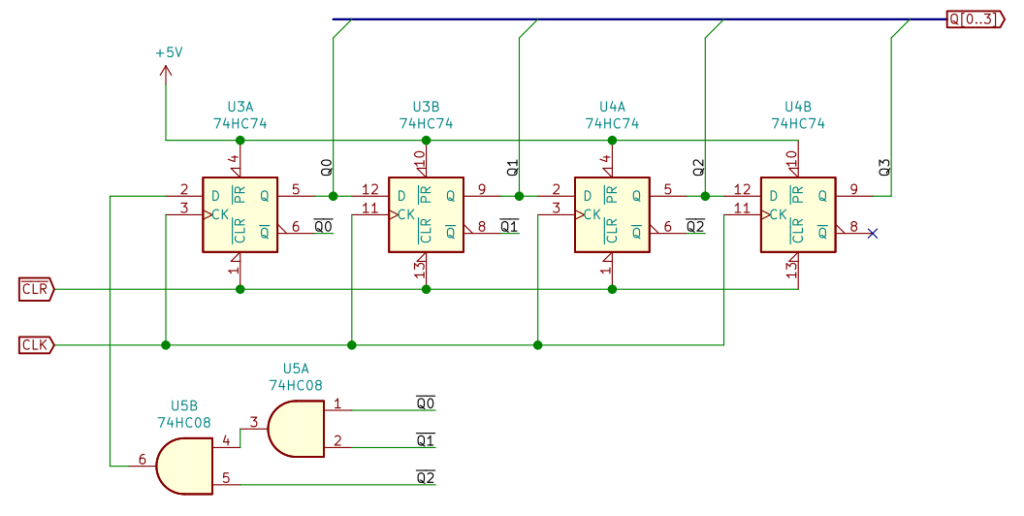
「すべての出力 (Q0, Q1, Q2) が 0 のとき 1 を出力 (D) する」を論理式にすると、
D = Q0 ⋅ Q1 ⋅ Q2
なので、フリップフロップの反転出力を AND すればよいとわかります。
ジョンソンカウンタと同様に、基本はシフトレジスタと同じです。AND ゲート 74HC08 を追加しました。
リングカウンタのシミュレーション
verilogHDL でシミュレーションしてみましょう。
- module TC74HC74A (
- input wire D, CK, PR, CLR,
- output reg Q, NQ
- );
- always @(posedge CK, negedge PR, negedge CLR) begin
- if(1'b0 == CLR) begin
- if(1'b0 == PR) begin
- Q <= 1'b1;
- NQ <= 1'b1;
- end
- else begin
- Q <= 1'b0;
- NQ <= 1'b1;
- end
- end
- else if(1'b0 == PR) begin
- Q <= 1'b1;
- NQ <= 1'b0;
- end
- else begin
- Q <= D;
- NQ <= ~D;
- end
- end
- endmodule // 74HC74A
- module RingCounter (
- input wire CLK, CLR,
- output wire [3:0] Q,
- output wire [3:0] NQ
- );
- wire D;
- assign D = NQ[0] & NQ[1] & NQ[2];
- TC74HC74A ff0(.D(D), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[0]), .NQ(NQ[0]));
- TC74HC74A ff1(.D(Q[0]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[1]), .NQ(NQ[1]));
- TC74HC74A ff2(.D(Q[1]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[2]), .NQ(NQ[2]));
- TC74HC74A ff3(.D(Q[2]), .CK(CLK), .PR(1'b1), .CLR(CLR), .Q(Q[3]), .NQ(NQ[3]));
- endmodule // RingCounter
37行目に ANDゲートを追加しています。
| Q[3..0] | Q3 | Q2 | Q1 | Q0 |
| 0x1 | 0 | 0 | 0 | 1 |
| 0x2 | 0 | 0 | 1 | 0 |
| 0x4 | 0 | 1 | 0 | 0 |
| 0x8 | 1 | 0 | 0 | 0 |
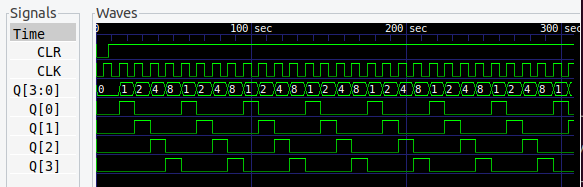
出力波形は、最初に入力した 1 が順番にシフトして、最終段から初段へ循環していることがわかります。
表3 が、出力コード表です。
リングカウンタの出力は、1 が常に 1ビットだけで、バイナリコードをデコードしたような信号になります。
また、リングカウンタは段数の分周回路になります。図11 は 4段なので 4分周回路です。
ブレッドボード
リングカウンタを実験中のブレッドボードです。
上は 5V電源回路。真ん中が、オペアンプを使ったクロック発振回路です。
下のブレッドボードは、左に押しボタンスイッチ回路と初期化回路の 74HC14。中央の 2個の ICが 74HC74 のシフトレジスタ。右が 74HC08。一番左は LEDの表示回路です。
まいどなんですが、シミュレーションだけじゃなくて、じっさいに回路を組んで試してみたよ、って話です (;´Д`)
後記
今回は、シフトレジスタと、それを使ったカウンタを勉強しました。
あとは、パラレル入力シリアル出力 (PISO) とか使ったことがないので、そのあたりも試してみたいです。でもその前に、マルチプレクサが必要かな。
過去記事一覧
論理回路に関するこれまでの記事をまとめておきました。
シフトレジスタ 74HC595 に関した記事も書いたことがあるので、こちらもご覧ください。
論理回路 / 基本的な論理回路
論理回路 / RSフリップフロップ
論理回路 / ゲート型 RS フリップフロップ
論理回路 / プライマリ・レプリカ型 RS フリップフロップ
論理回路 / Dフリップフロップ
論理回路 / JK フリップフロップ
論理回路 / 分周回路・カウンタ回路
論理回路 / 4進同期カウンタ (2bit)
論理回路 / 8進同期カウンタ (3bit)
論理回路 / 16進同期カウンタ (4bit)
論理回路 / 10進同期カウンタと 7セグメントLED
論理回路 / 半加算器と全加算器
論理回路 / 4ビット加算器の構成とシミュレーション
論理回路 / 4ビット加算器をロジック IC でつくる
加算器でカウンタを作る / 構成とシミュレーション
加算器でカウンタを作る / 16進カウンタ
加算器でカウンタをつくる / 10進カウンタ