Dフリップフロップを使ったカウンタ回路をつくってみました。
2進~10進同期カウンタは、前回の記事を参照ください。
JKフリップフロップを使ったカウンタ回路は下記を参照ください。
11進~16進同期カウンタ
Dフリップフロップを使用した 11進~16進同期バイナリアップカウンタの回路例です。
フリップフロップとかカウンタとか真理値表とかカルノー図とか、基本的なことは教科書みるか、グーグル先生に尋ねてください。
なお、シミュレーションは論理式について行なっており、回路図と連動していません。回路はじっさいに製作しておらず、動作を確認していません。
11進カウンタ
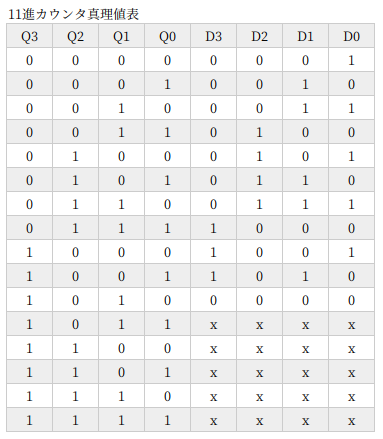
11進カウンタです。
考え方はこれまでとかわりありません。
奇数の n進カウンタなので、ちょっと面倒くさいです。7進とか 11進とか、素数の n進カウンタって、さらに面倒くさい、ですか?

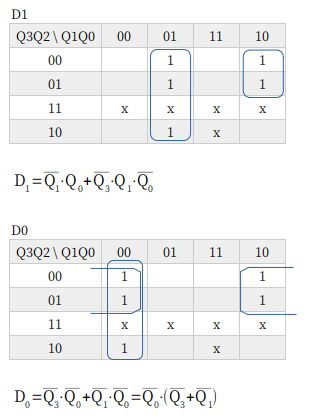
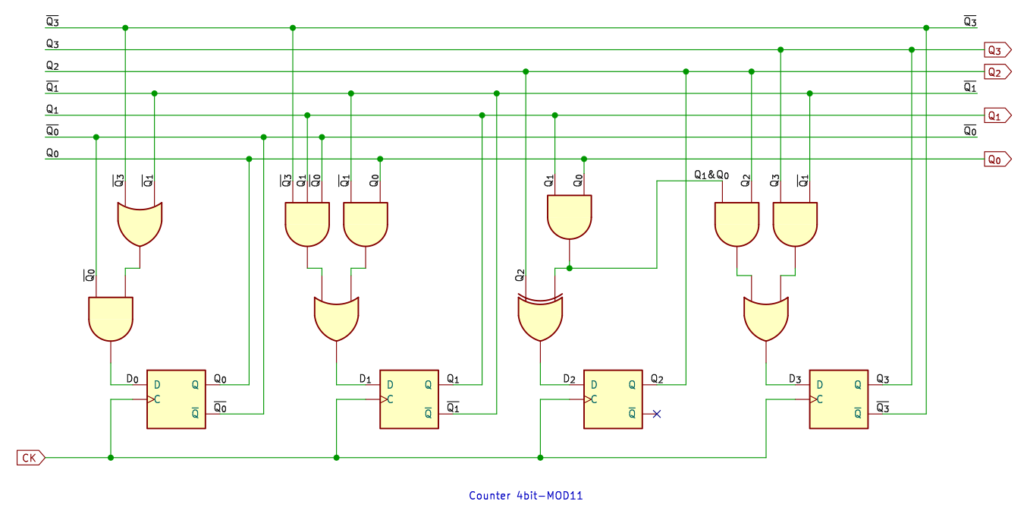
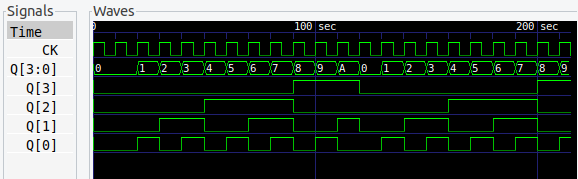
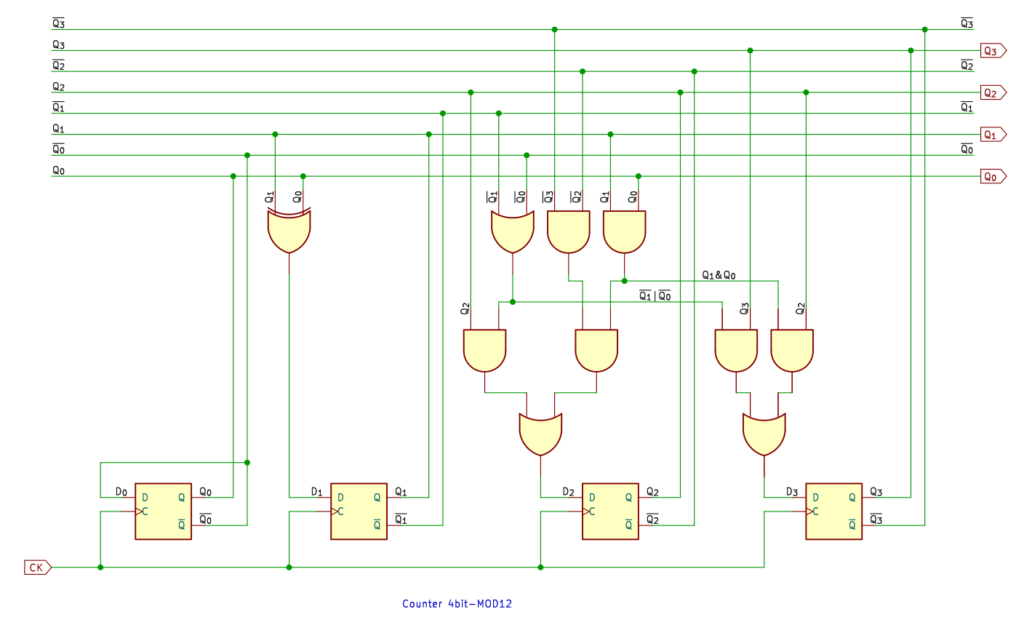
12進カウンタ
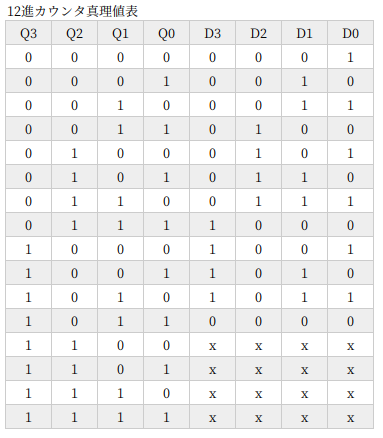
12進カウンタ。
なんかねぇ、もう少しどうにかならないか考えたんですけど、どうにもならなかった。素直に論理式をつくって、ゲートを共用できるところを共用した、という感じです。
うまい方法ないですか? あったら教えてくださいませ。

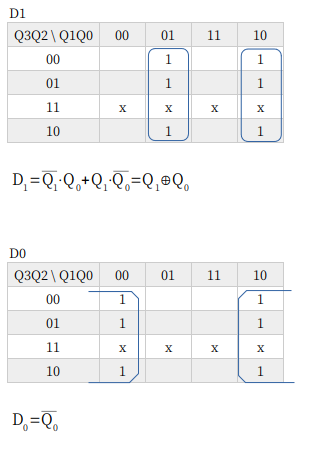
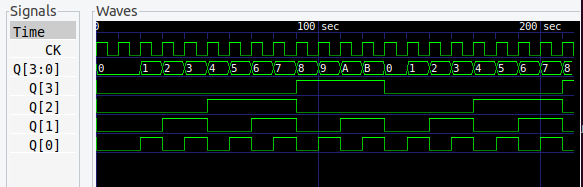
13進カウンタ
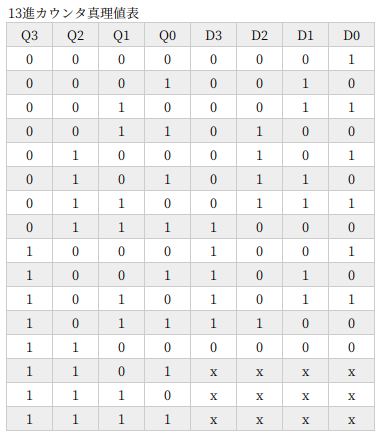
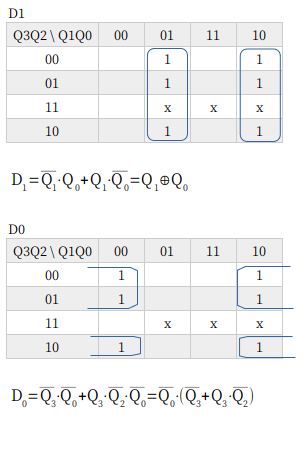
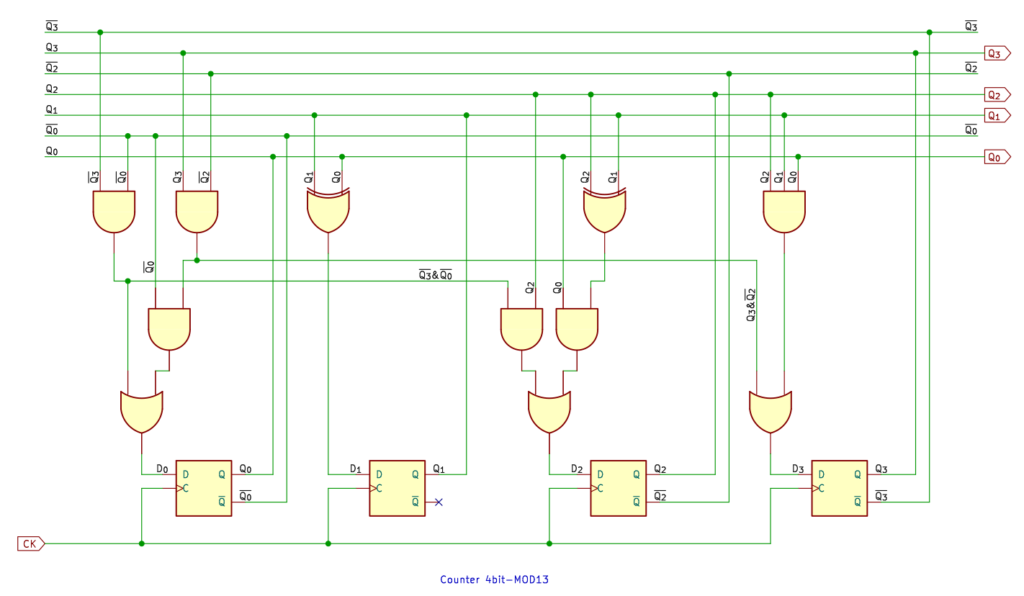
13進カウンタも、なんかこうスッキリしないですが、こんなもんでしょうか。
D0 は、論理式は Q0 でくくってみましたが、ゲートを共用できるのでくくる前の式で回路をつくってます。どっちにしても大差ないのですが、部品箱に 3入力 AND がないので、ついつい避けるほうにいってしまうんですねぇ。

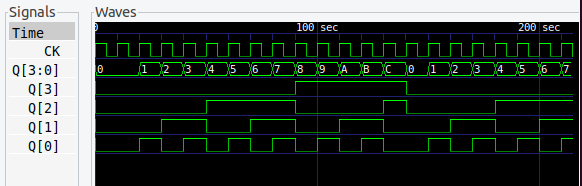
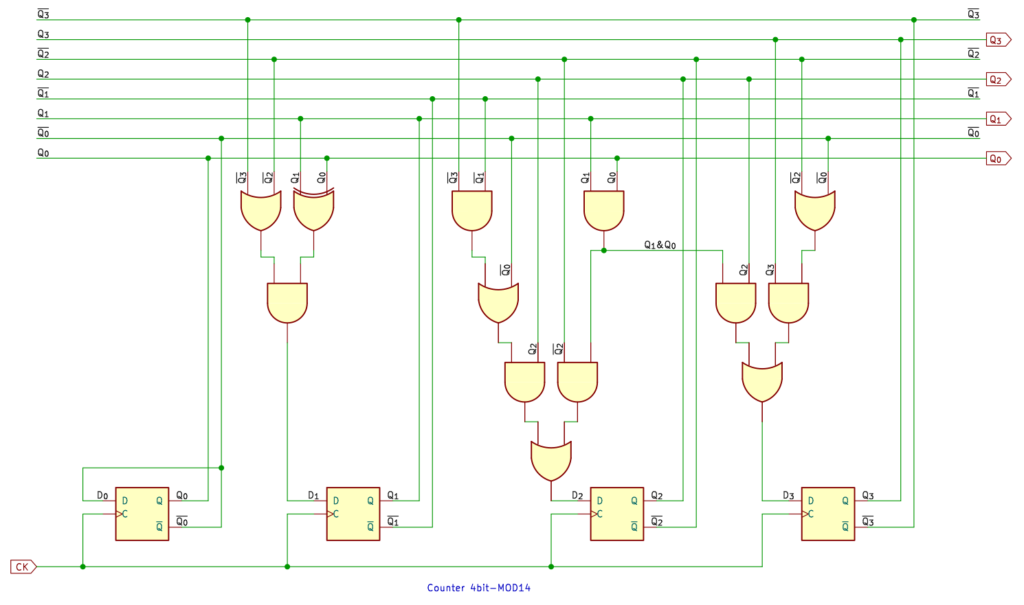
14進カウンタ
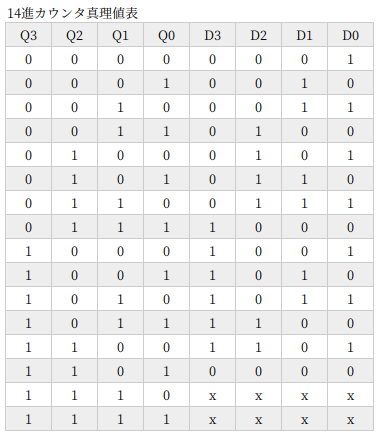
ますます混迷度が増す 14進カウンタです。もうね、素数 n進とか関係ないことがわかりました。
いろいろ悩んでみたんですけど、まぁ基本的に素直に論理式どおりにするのが、いちばんわかりやすいんじゃないかと思います。
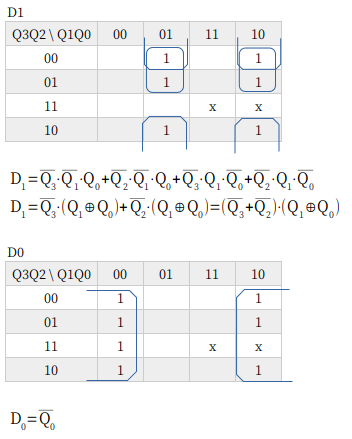
D1 に関しては、don’t care を 0 として排他的論理和にしています。カルノー図のこのパターン、覚えておきましょ。
ちなみに、Q1Q0 が 00 と 11 になるときは、否定排他的論理和 XNOR になるので、そんなパターンも頭の片隅にとどめておきましょう。

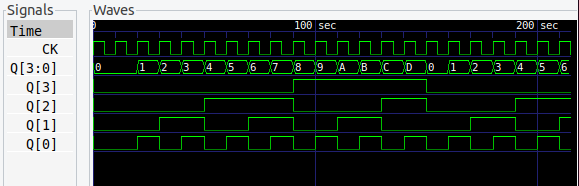
15進カウンタ
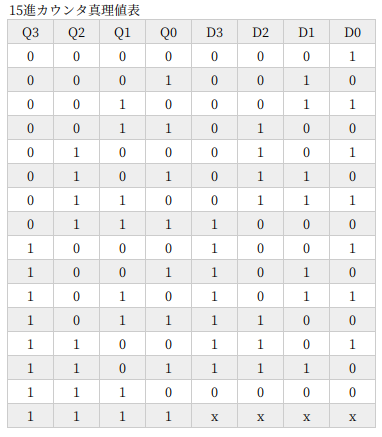
15進カウンタです。
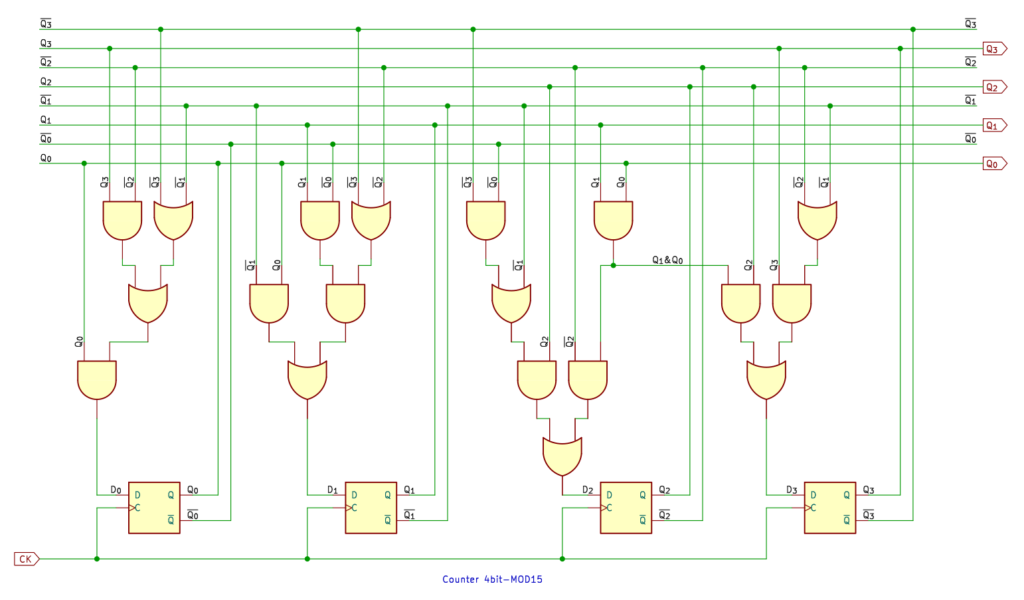
もうね、むずかしく考えるのはやめましょう。論理式どおりに回路を描きました。
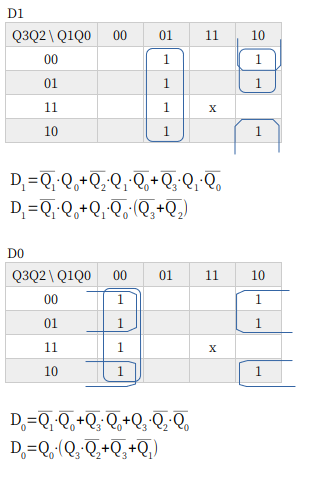
D1 は、14進カウンタと同じように XOR を使う方法もあります。まぁ、メリットないですけど。
D0 は 3入力 OR でいいんですけど、KiCad にシンボルみつけられなかったので、2入力つかってます。

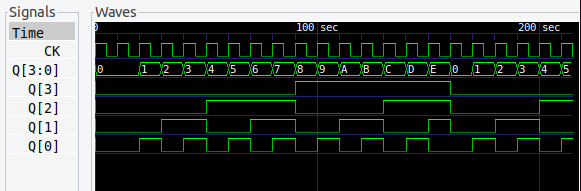
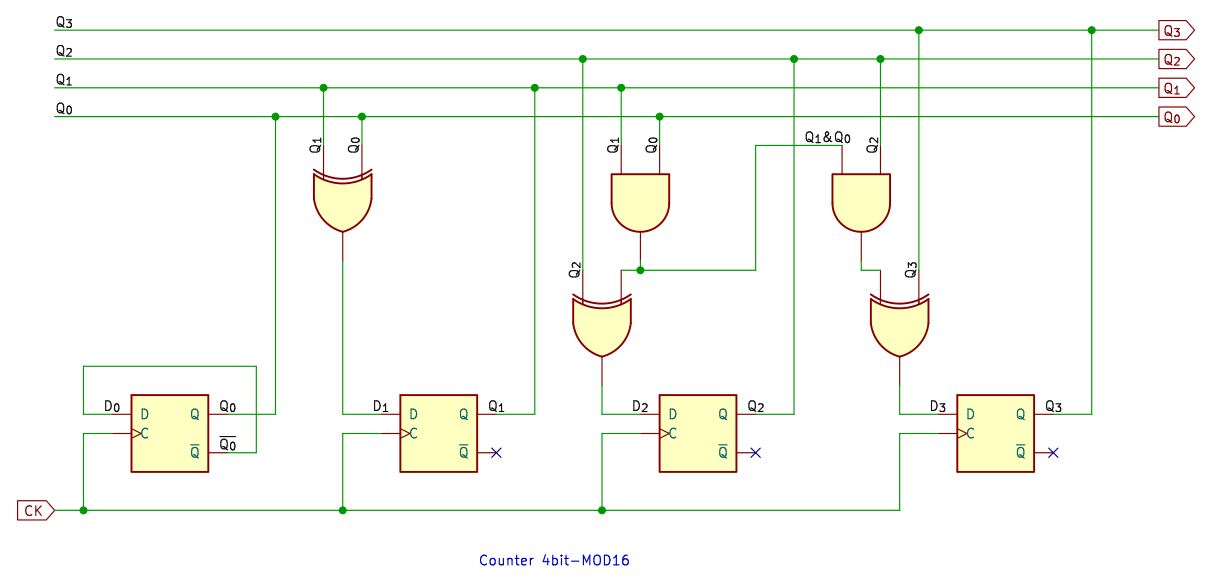
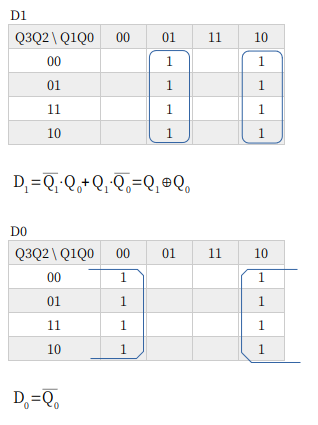
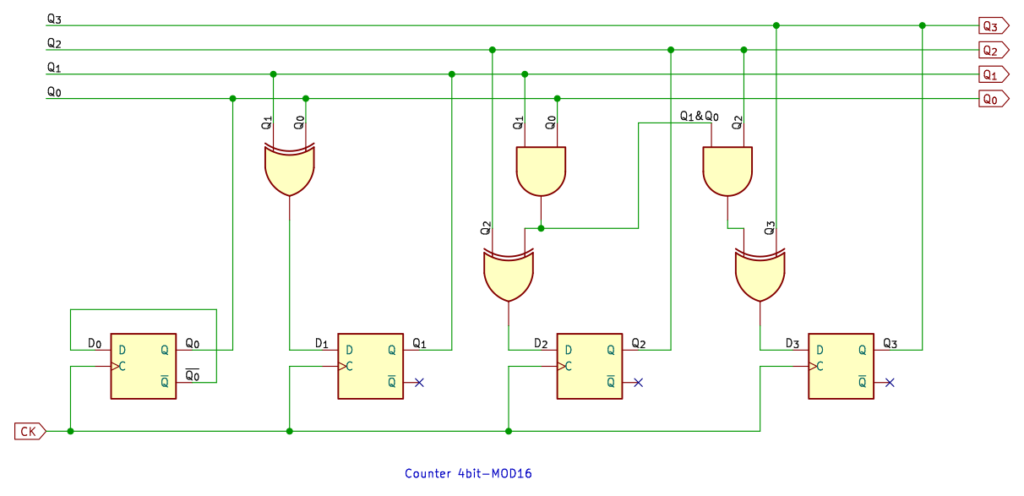
16進カウンタ
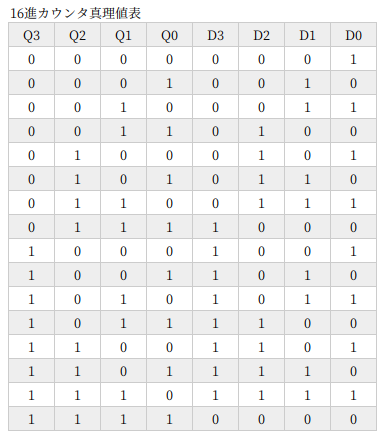
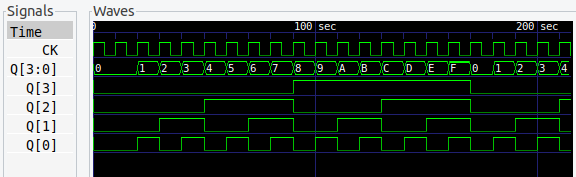
4ビット、最後のカウンタは 16進カウンタです。
JKフリップフロップでつくった 16進カウンタ (参考記事) に、XOR を追加して Dフリップフロップに置き換えた回路。4進、8進カウンタと同じです。すっかり簡単になっちゃいますねぇ。
もちろん、真理値表から論理式を求めても同じ結果になります。D2、D3 はちょっとややこしいですけど、同じパターンなので、論理式の変換はたやすいと思います。

ちなみに、加算器を使って 16進アップダウン・カウンタをつくったことがあります。あわせてご覧ください。
後記
前回の 2進~10進カウンタに引き続き、Dフリップフロップを使った同期カウンタ、11進~16進のバイナリアップカウンタの回路をつくってみました。
JKフリップフロップに比べて、Dフリップフロップをつかったカウンタの組み合わせ回路は複雑になります。12進、13進あたりはまぁいいとしても、14進、15進となるともう面倒くさい。が、もっと複雑な組み合わせ回路はいくらでもあるし、めげてちゃいけませんな。
5ビット以上のカウンタになると、カルノー図で論理式を求めるのもちょっと大変になります。方法は過去記事にちょこっと書いてますので参照ください。6ビットは、同じように上下左右に重なっていると考える … もうやめましょう。別の方法を考えたほうがよさそうです。