今回は、Dフリップフロップを使った 60進カウンタ (BCD出力同期カウンタ) をつくってみます。
60進カウンタは、これまでデジタル時計をつくるために何度もやっています。まぁ基本的にはそれと同じですが、今回は、同期設計についてちょっと厳格にやってみよう、というところでしょうか。
この記事の回路では、カウンタを動作させるイネーブル信号 EN でクロック信号 CK を制御、つまり EN が HIGH のとき CK を有効にし、LOW のとき無効にすることでカウンタの動作を制御していました。
でも、同期回路のクロック信号はフリップフロップのクロック入力にだけ入れる、というのがルールじゃないかな。逆に言えば、フリップフロップのクロック入力にはクロック信号だけを入れるべきで、イネーブル信号を入れてはいけないんじゃないか。また、クロック信号を反転させると同期していると言えなくなるんじゃないか。と。
そこで、クロック信号はクロック入力にだけ入れ、イネーブル信号は組み合わせ回路に取り込んでカウンタ回路を設計してみよう、というのが今回の目的です。
60進同期カウンタ (BCD出力)
今回設計するカウンタは 10進 x 6進カウンタの組み合わせですので、BCD出力で 0~59 をカウントする同期カウンタです。1Hzのクロックを入力すると 60秒間をカウントしてくれます。
ちなみにこのやり方は、複数のカウンタを組み合わせて n進カウンタをつくる、という応用ができます。たとえば 16進を 2段にすれば 256進カウンタになります。10進 x4段にすると BCD 4桁のカウンタができます。
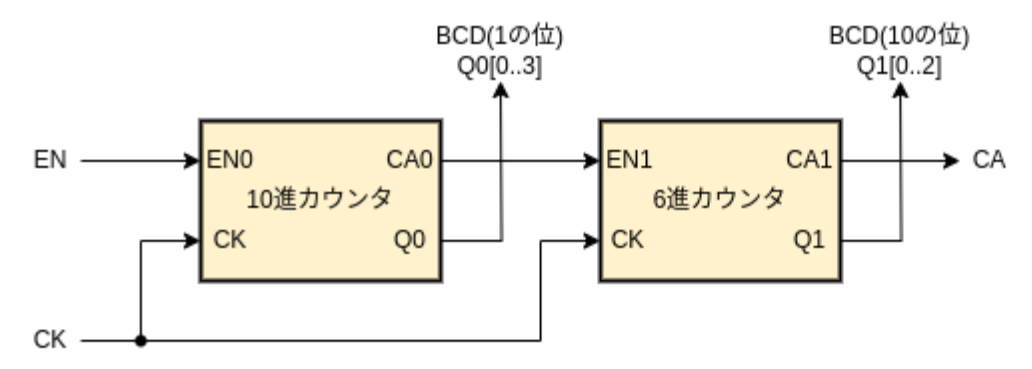
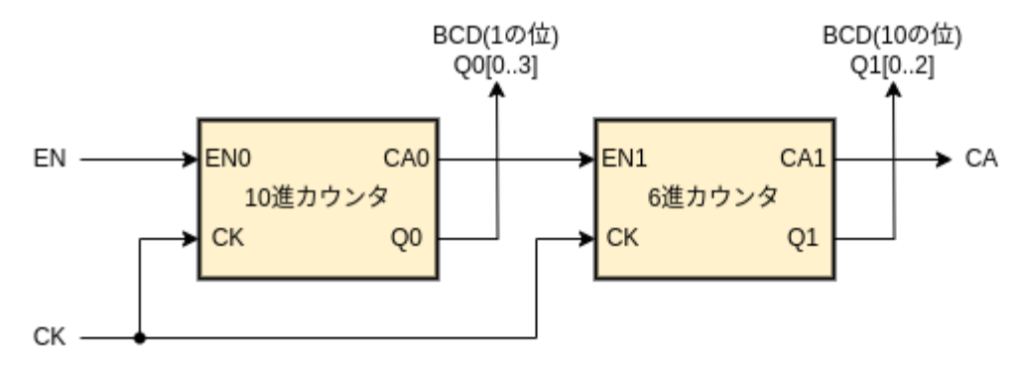
構成図
カウンタは 10進と 6進の同期カウンタです。イネーブル信号 EN が HIGH のときにカウント動作し、LOW では出力を保持し停止します。
10進カウンタは、1の位の 0~9 (Q0[3..0]) を出力します。桁上がり信号 CA0 は、Q0=9 で EN0=1 のとき出力されます。
6進カウンタは 10の位の 0~5 (Q1[2..0]) を出力します。CA1 は、Q1=5 で EN1=1 のとき出力されます。
10進カウンタの桁上がり信号 CA0 を 6進カウンタのイネーブル信号 EN1 に入力することで、全体として 60進カウンタとなり、出力が 59 のときに CA が出力されます。
10進カウンタの論理式
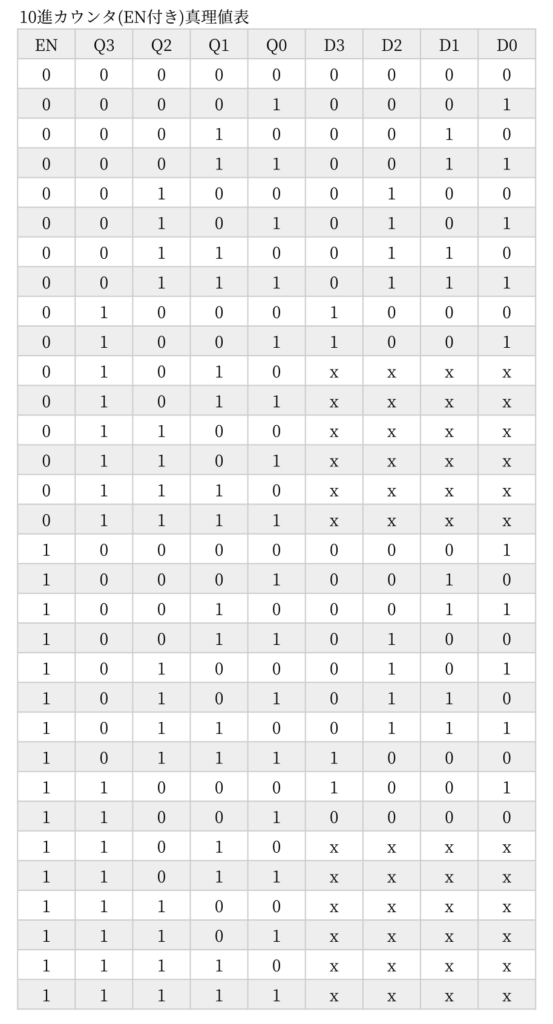
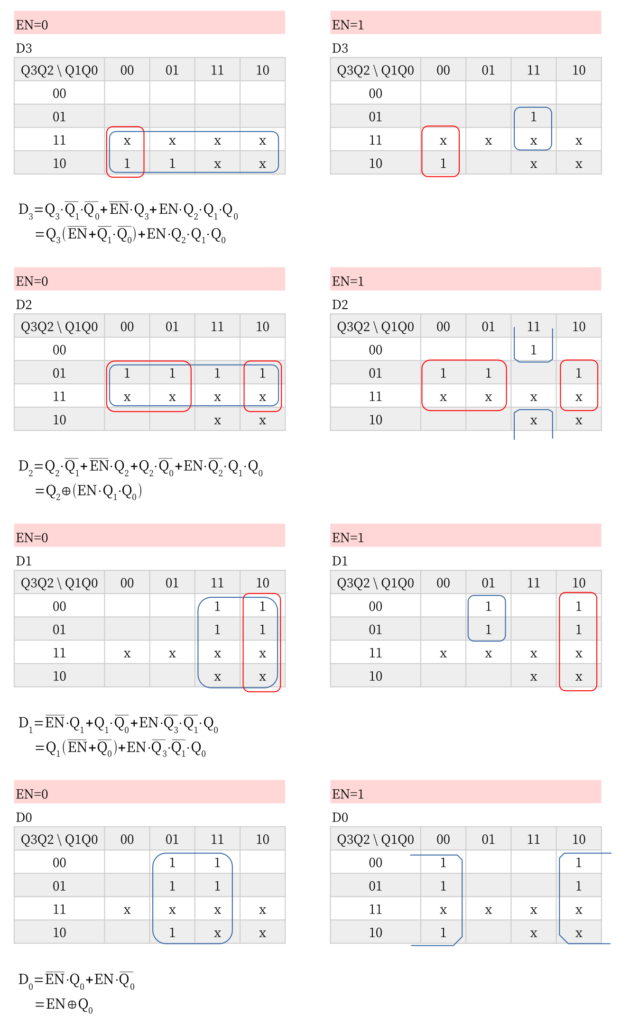
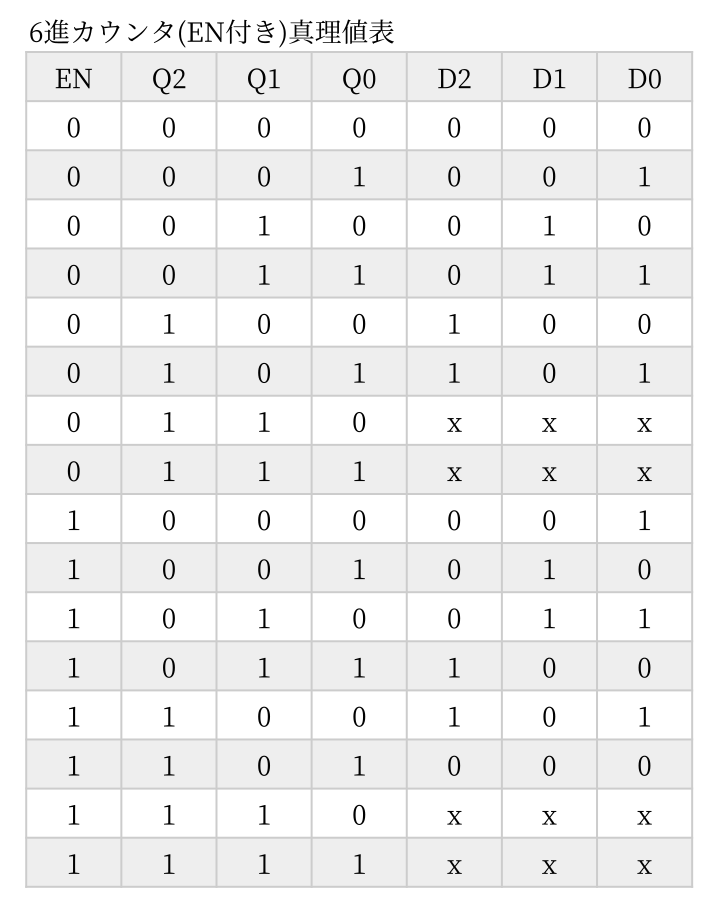
10進カウンタの真理値表から論理式を求めます。
真理値表は EN を加えて 5変数です。EN=0 のときと EN=1 のときのカルノー図をそれぞれに作り、それを重ね合わせて括ります。赤枠が上下に括られているところ、青枠はどちらかだけの場合です。
6進カウンタの論理式
6進カウンタの真理値表から論理式を求めます。
こちらも EN を加えていますが、4変数なのでこれまで同様にカルノー図を作ります。
桁上がり信号 CA の出力
桁上がり信号 CA は、10進カウンタでは Q0=9 (Q0[0..3]=0b1001) かつイネーブル信号 EN0=1のとき、6進カウンタでは Q1=5 (Q1[0..2]=0b101) かつ EN1=1 のときに出力します。60進カウンタとしてみたときは Q=59 で出力されることになります。
論理式は、
CA0 = EN0⋅Q0[3]⋅Q0[0] CA1 = EN1⋅Q1[2]⋅Q1[0]
わかりにくければ、真理値表に加えて考えてみると良いと思います。
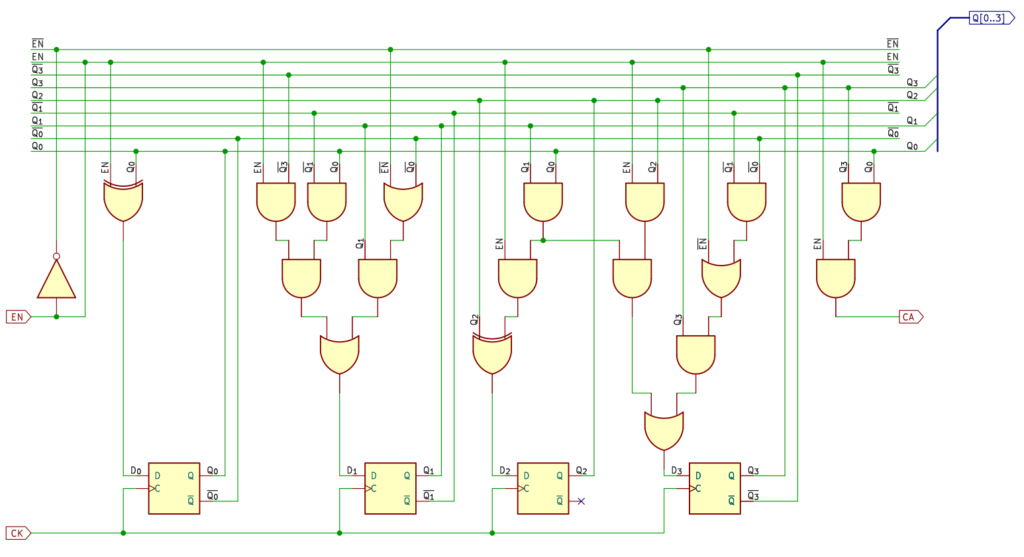
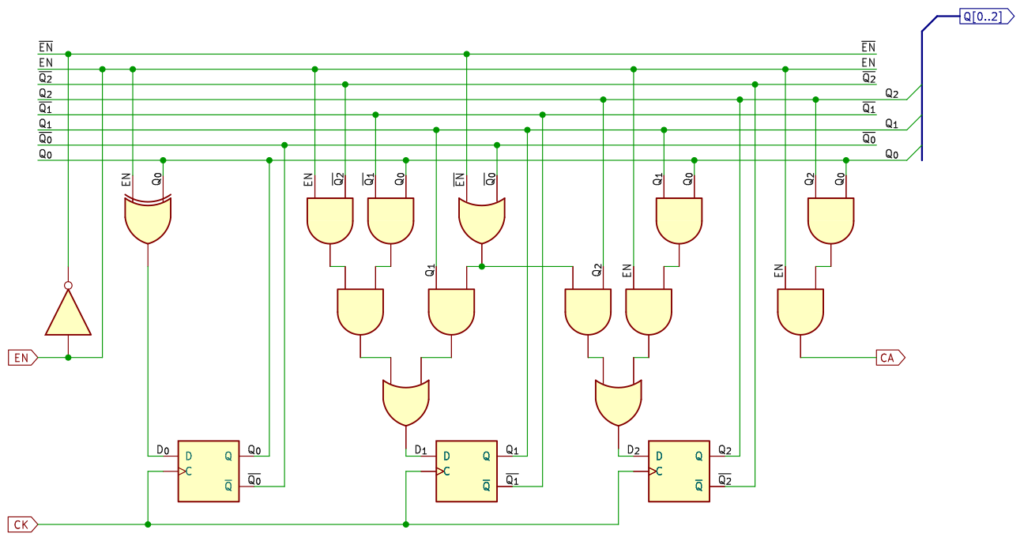
10進カウンタ回路図
10進カウンタの回路図です。論理式をそのまま回路にしていますので、特に説明することはありません。イネーブル信号 EN 入力と桁上がり信号 CA 出力の回路が含まれています。
クロック信号はフリップフロップのクロック入力にだけ入り、クロック入力にはクロック信号だけが入るという同期設計のルールどおりになりました。
6進カウンタ回路図
6進カウンタは 3ビットですが、考え方は10進カウンタと同様です。
シミュレーション
60進カウンタを VerilogHDL でシミュレーションしました。
Q1 が 10の位、Q0が 1の位です。0~59 の値を BCD で出力していることが確認できました。桁上がり信号 CA は 59 のときに出力されています。

なお、シミュレーションは論理式について実行しており、回路図には連動していません。回路はじっさいに組み立てていませんので、正常に動作するかどうかの検証はしていません。あしからず m(_ _;)m
3600進カウンタ (秒・分カウンタ)
60進カウンタを 2段つなぐと 3600進カウンタができます。
構成図
3600進カウンタの構成は、10進 – 6進 – 10進 – 6進と配置して、それぞれの桁上がり信号を次のイネーブル入力につなぐだけです。
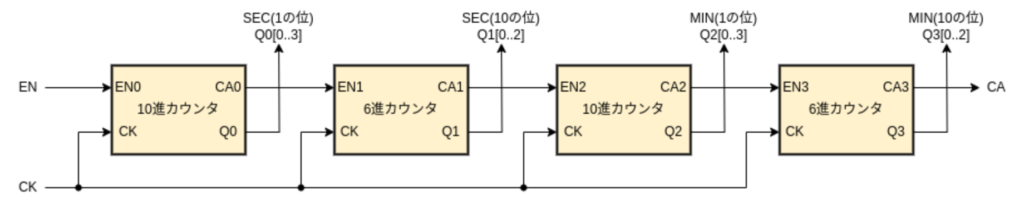
クロック信号として 1Hz (周期が 1秒) のパルス信号を入力すると 60分 (00分00秒~59分59秒) をカウントするカウンタ回路になります。これは時計などに利用できます。
シミュレーション
図6 は、3600進カウンタの全体のようすです。
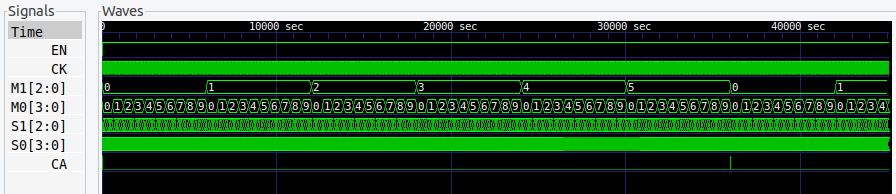
クロック信号などは細かくてつぶれてしまっていますが、M1、M0 が 0~59 をカウントしているのがわかります。M1、M0 は、それぞれ分表示の 10の位、1の位です。59分までカウントし、細くてわかりにくいですが、桁上がり信号 CA が出力されています。
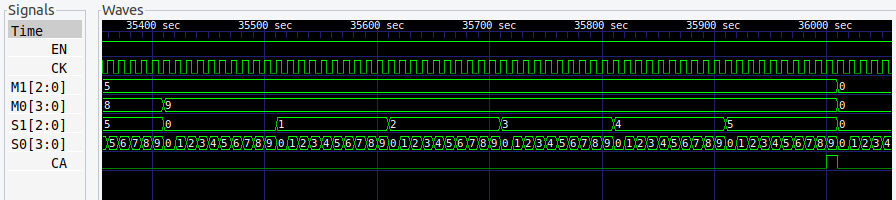
CA を出力しているあたりを拡大してみると、59分59秒 (3599クロック目) で CA=1 となっていることがわかります。これをさらに上位のカウンタに渡せば、1時間毎のカウントをさせることができます。24進カウンタで時をカウントさせれば 1日を刻むことができますね。
後記
冒頭にも書きましたが、60進カウンタはデジタル時計の製作でなんどもとりあげています。基本的な考え方は同じですので、過去記事も参考にしていただければと思います。
今回あらためて取り上げたのは、カウンタの同期設計の考え方をアップデートするためです。
同期設計についてはわからないことばかりですが、少なくとも、クロック信号はフリップフロップのクロック入力だけに入れること、クロック入力にはクロック信号以外を入れないことをルールとしましょう。
さらに厳格に考えるなら、ひとつの発振器で作られた同じクロック信号でも、分配している配線や回路で遅延が発生すれば同期しているとみなせなくなる。反転させれば、同期しているかあやしくなる。ましてや分周したりすれば遅延が発生し、非同期となってしまう。こうしたことがきちんと管理されてはじめて「同期している」と言えるのでしょう。
俺が扱っている程度の回路では、いまのところそこまで厳格に考える必要はなさそうですけど、基本的な考え方は守っていきたいと思います。