Dフリップフロップを使ったカウンタ回路をつくってみました。
11進~16進同期カウンタは、続きの記事を参照ください。
JKフリップフロップを使ったカウンタ回路は下記を参照ください。
2進~10進同期カウンタ
Dフリップフロップを使用した 2進~10進同期バイナリアップカウンタの回路例です。
フリップフロップとかカウンタとか真理値表とかカルノー図とか、基本的なことは教科書みるか、グーグル先生に尋ねてください。なお、シミュレーションは、verilogHDL によって論理式について行なっており、回路図と連動していません。回路はじっさいに製作しておらず、動作を確認していません。
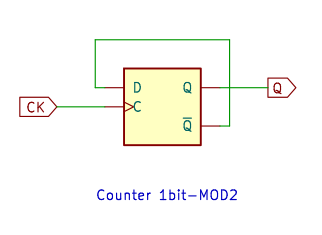
2進カウンタ
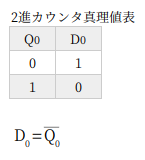
2進カウンタです。
というか、クロックが入るたびに出力がトグルするだけの回路。これを並べると非同期カウンタ (リプルカウンタ) になるけれど、ここでは扱いません。
出力 Q を入力 D にもどすことで Tフリップフロップになる、基本的な回路です。偶数の n進カウンタは LSB が 1 と 0 の交互になるから、初段は必ずこの回路になります。
シミュレーション結果は、Tフリップフロップの出力そのものです。

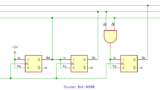
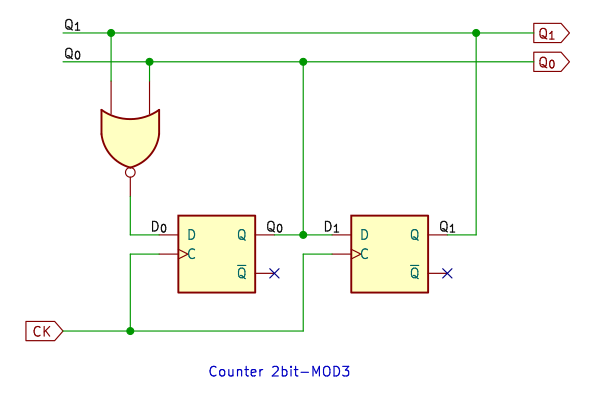
3進カウンタ
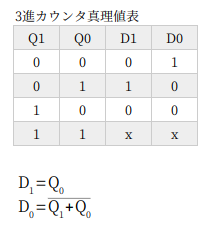
Dフリップフロップの場合、次の出力の状態 Qn+1 はそのまま D の入力値になる。
現在の出力が 00 ならば、次の状態は 01 になるから、入力は 01。さらにその次の出力は 10 だから、入力も 10。3進カウンタなので、出力 10 の次は 00 にもどし、出力 11 は don’t care にする。
そうやって真理値表を埋めていきます。
真理値表をじっと眺めていると、D1 は Q0 と等しい、D0 は Q1 と Q0 の NOR だと見えてきます。見えるでしょ? don’t care は、0 でも 1 でも、都合のよいようにする。ここでは、D1 は 1 に、D0 は 0 と考えればそうなります。
論理式より、Q1 と Q0 を NOR して D0 につなぐ、という回路ができる。D1 は Q0 に等しいのだから、そのままつなげばよろしい。
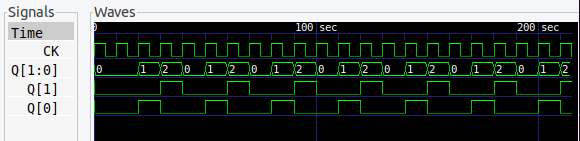
シミュレーション結果は、ちゃんとワルツしてます。
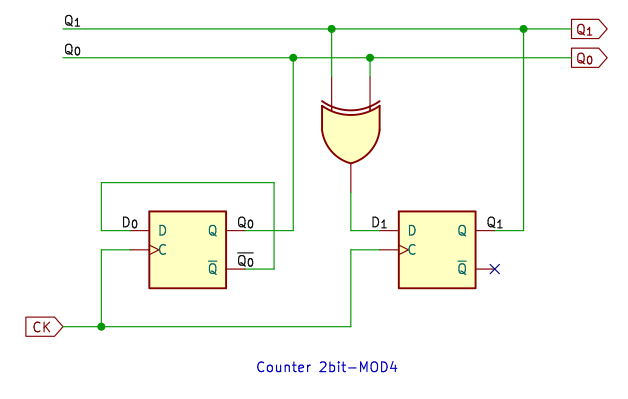
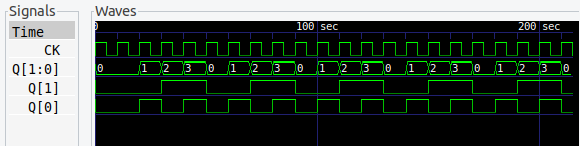
4進カウンタ
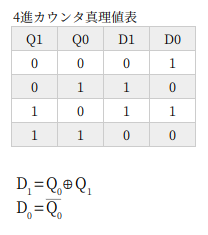
3進カウンタと同様に、真理値表をじっと眺めると、見えてきます。主加法標準形とかでもいいかもです。カルノー図をつくるほどではない。
D1 は排他的論理和 XOR ですね。入力が同じなら 0、異なっていれば 1 を出力する。
D0 は Q0 を NOT する。偶数のカウンタだから、初段は Q0 を D0 にもどす Tフリップフロップになるんです。
この回路は、ネットでもみつけることができます。でも、少ないんですよ、Dフリップフロップ使用のカウンタ回路例って。
みなさん、JK がお好きなようで (;´Д`)
シミュレーション結果は、なんとなくバイナリカウンタらしくなってきました。
5進カウンタ
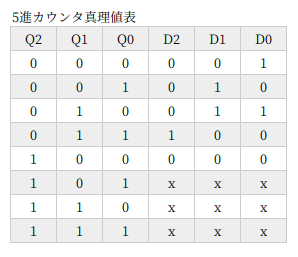
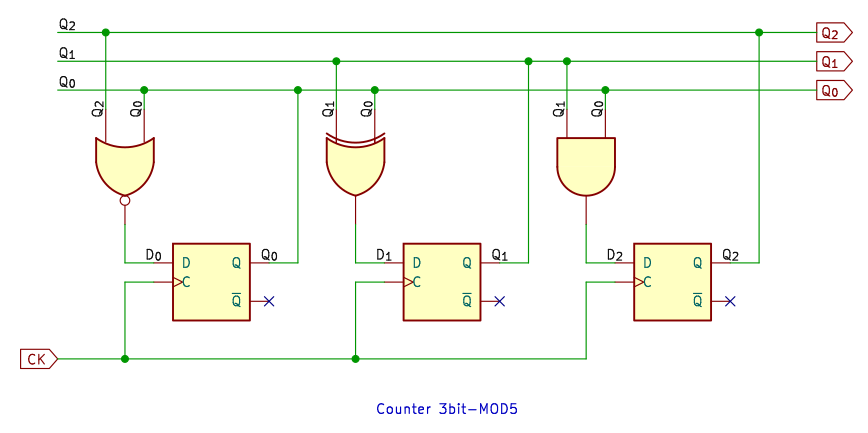
5進カウンタから 3ビットになり、Dフリップフロップが 1つ増えます。
これまで同様に、真理値表を眺めているといろいろ見えてきますけど、考えている間にカルノー図書けちゃうので、カルノー図で論理式を求めました。

Dフリップフロップを使うカウンタ回路では、排他的論理和 XOR がよくでてきます。XOR を使うと、Dフリップフロップを JKフリップフロップのように動作させることができるので、組み合わせ回路が簡単になるんです。
このことについては、8進カウンタの項に書きます。
D0 は、AND でも NOR でも、どちらでもいいです。ここでは、反転出力 Q を使わなくてもいいので、NOR にしました。
シミュレーションは、ん〜、♫ Take Five
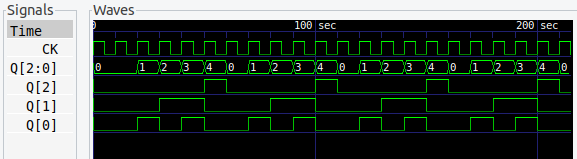
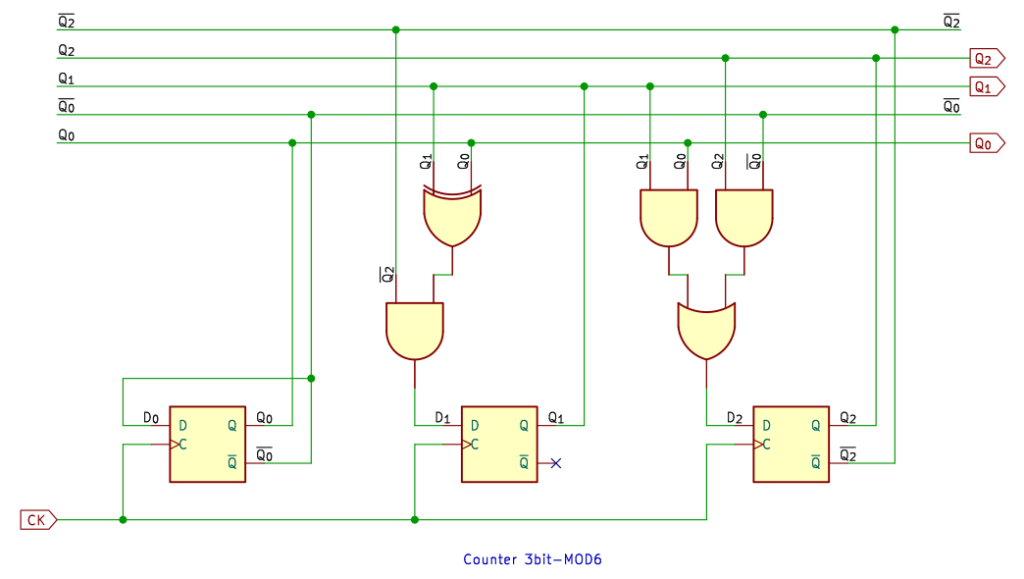
6進カウンタ
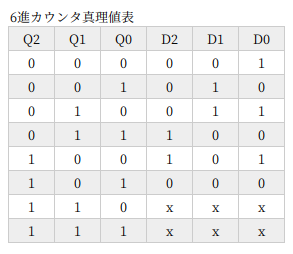
6進カウンタ。これと 10進カウンタをつなぐと 60進カウンタになります。デジタル時計の製作 (参考記事) で、さんざんやりましたねぇ。
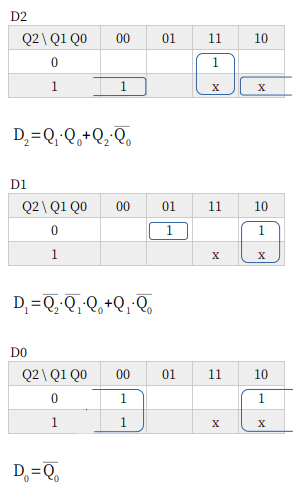
D2 はセレクタです。Q0 が 1 ならば Q1 を、0 ならば Q2 を出力する。
D1 は、左のカルノー図がふつうのやり方です。が、あえて don’t care を 0 と考えて、下のようにしました。

こうすることで、XOR で構成できます。どっちがいいかはお好みですが、Dフリップフロップには XOR がお似合いじゃないかしら。
D0 は、考えるまでもなく Tフリップフロップで決まりです。
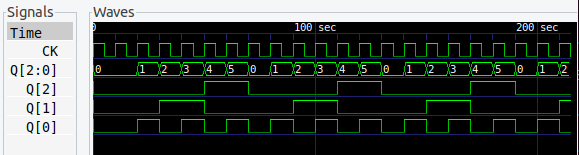
7進カウンタ
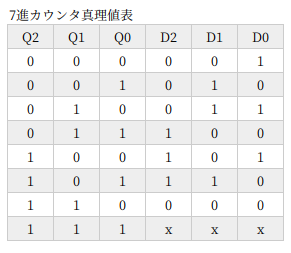
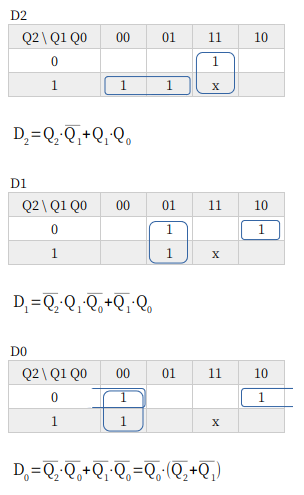
ラッキー7 とかいいますが、カウンタ回路としては複雑になってきます。なんだか面倒くさいやつ。
D2 はセレクタです。これ以上無理する必要ないです。
D1 は、なんだか XOR にできそうですけど、逆に複雑になってしまいます。おとなしく 3入力 AND を使いましょう。
D0 も、奇数 n進なので面倒くさい。
Q2⋅Q0 を D1 と共通で使うって手もあるんですけど、D0 のゲートが増えるので、全体としては変わらんです。
うまい方法があったら、教えてくださいませ。
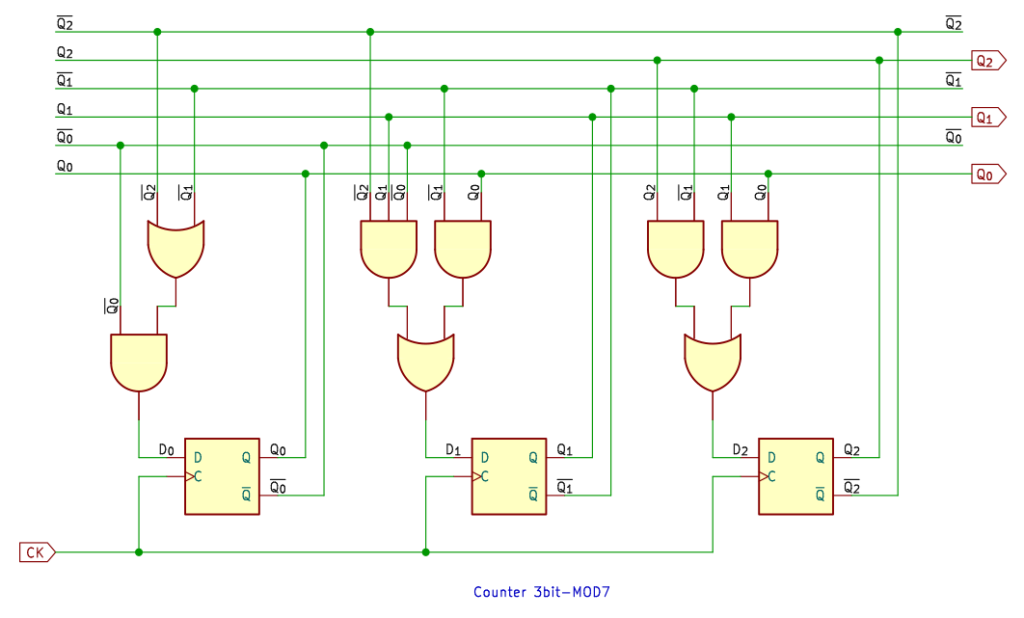
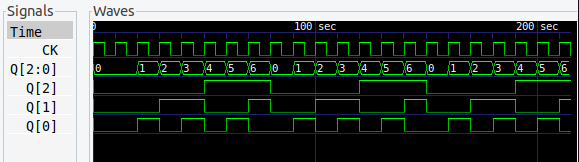
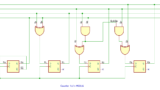
8進カウンタ
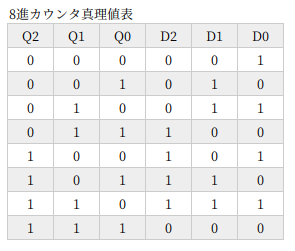

8進カウンタ。23 できりがいいせいか、回路はちょっと簡単になります。
4進カウンタでもそうですけど、JKフリップフロップでつくった回路 (参考記事) に、XOR をプラスした形になっています。どちらも、JKフリップフロップの J と K をつないでいるところに注目してください。
出力 Q を XOR の片方の入力にもどし、もう一方を入力 J とします。こうすると、J に 1 が入るとクロックのたびに Q が反転し、0 のときは Q は前の状態を維持し変化しない、という動きをします。
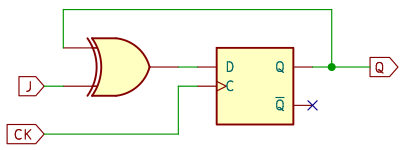
これは、JKフリップフロップの J と K をつないだときの動作と同じなので、Dフリップフロップへの置き換えができます。
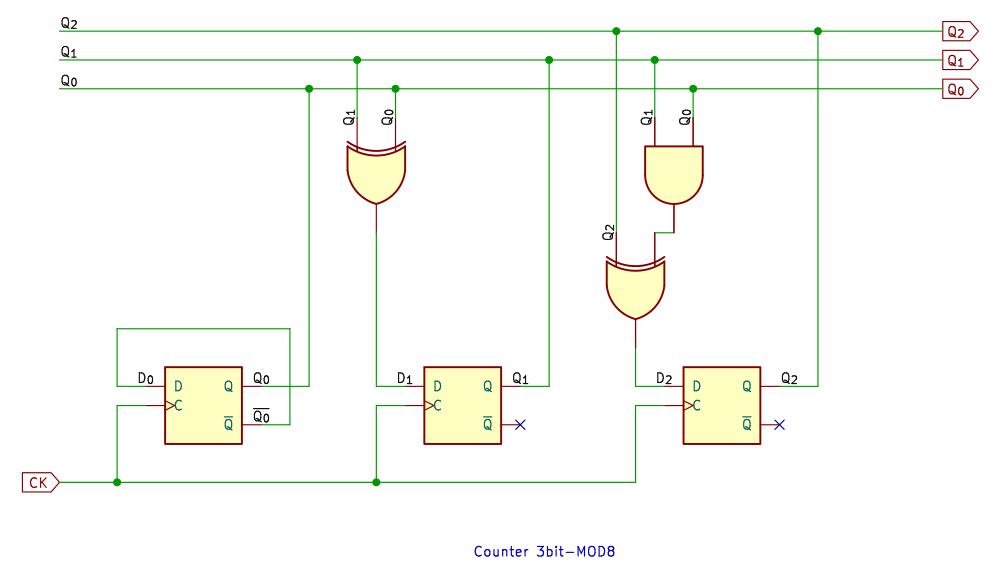
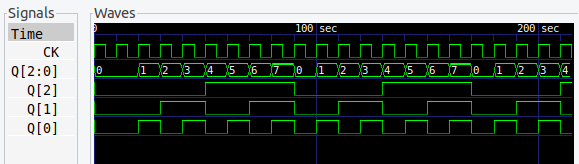
9進カウンタ
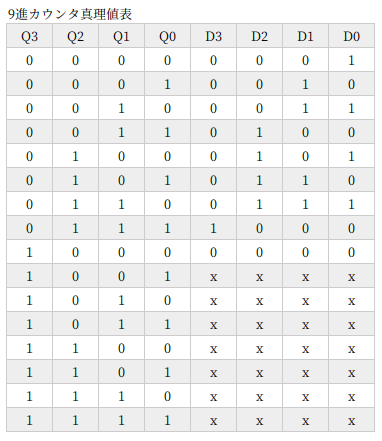
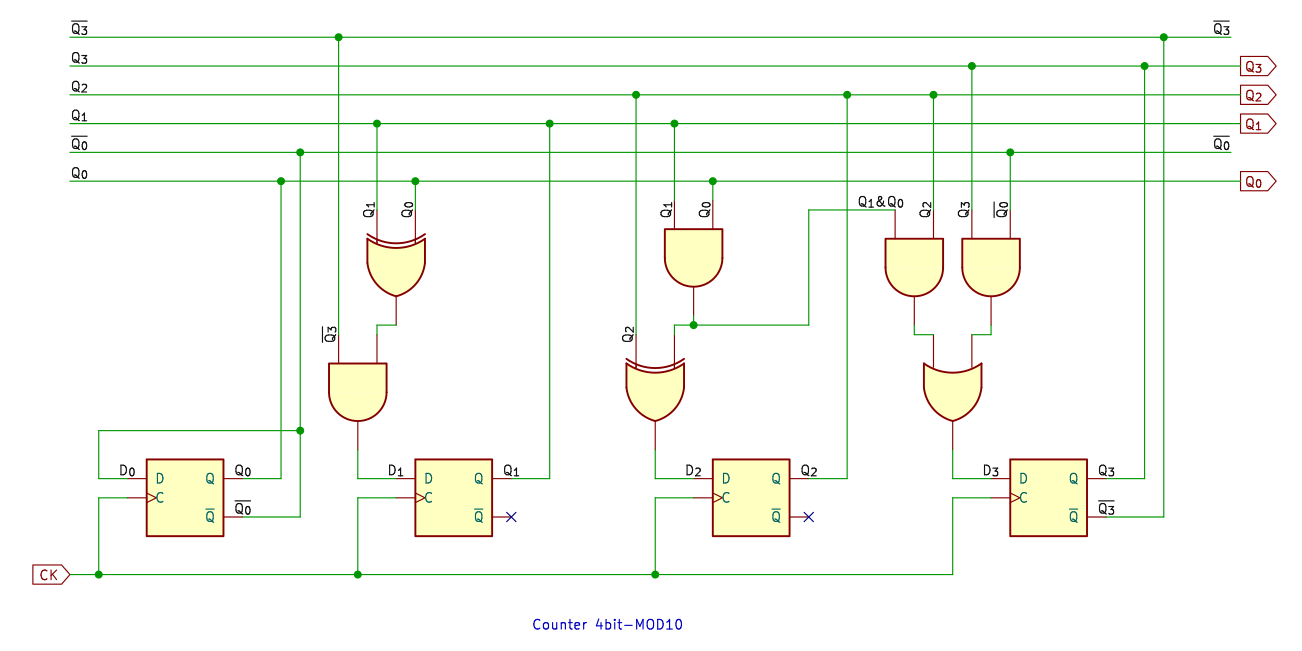
9進カウンタから、フリップフロップがさらに増えて 4ビットになります。
真理値表も大きくなってきますが、don’t care が多いので、まだ楽かな。大きくても、やることはこれまでとかわりありません。
Q1⋅Q0 を D3 と D2 で共用しています。もちろん、3入力 AND でもいいです。

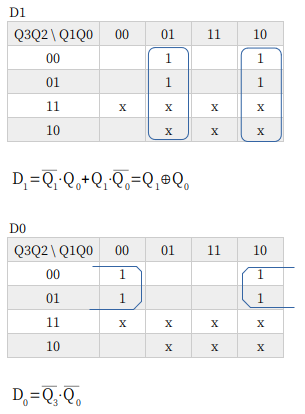
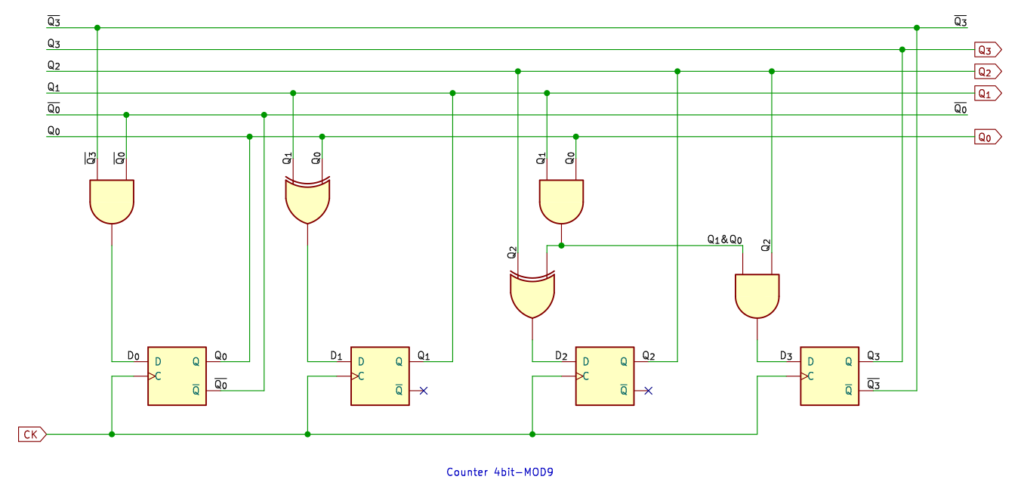
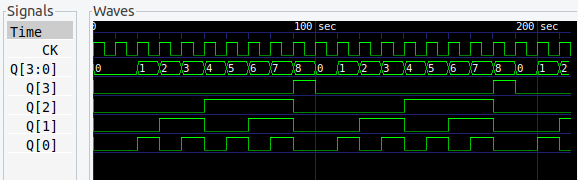
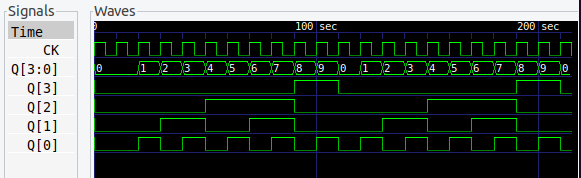
10進カウンタ
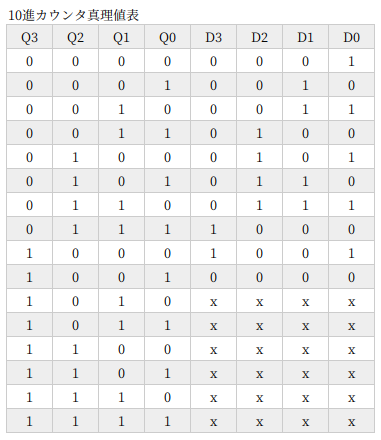
BCDで出力するために必要になる 10進カウンタです。これもデジタル時計の製作 (参考記事) で、さんざんやりました。
やることに、なんらかわりはありません。せっせとカルノー図書いていくだけです。あ〜、勉強ですから、自分で鉛筆持ってやるんですよ。

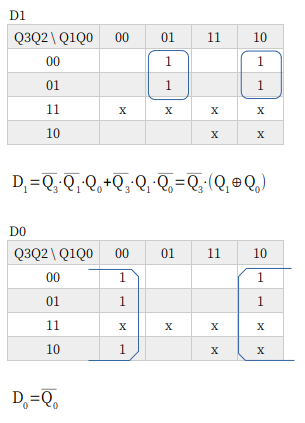
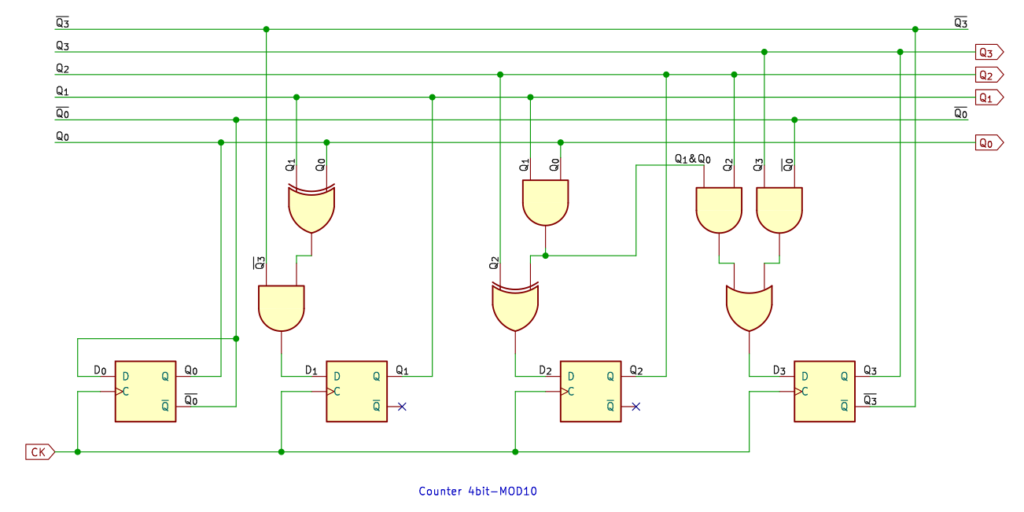
ちなみに、加算器を使って 10進アップダウン・カウンタをつくったことがあります。あわせてご覧ください。
後記
カウンタ回路の勉強をしはじめた頃から、おりにふれ参考にさせていただいたサイトがありました。そこには、フリップフロップの動作から真理値表の作り方、論理式の求め方、カルノー図の書き方などなど、とても詳しく解説されていて、たくさんのカウンタ回路例があり、それぞれ動作のシミュレーションが示されていました。
最初はわからないことだらけでしたが、グーグル先生にも教えてもらいながら、だんだん理解できるようになっていきました。俺のカウンタ回路作成のバイブルのようなサイトでした。
が、いつからか、アクセスしようとすると 404エラーに。検索しても見つからなくなりました。
そんなサイトを、俺は自分でつくることはとてもできません。でも、そこで学んだこと、たくさんのグーグル先生に教えてもらった知識で、そこにあったようなたくさんのカウンタ回路例をつくってみたかった。
今回は、Dフリップフロップを使った同期カウンタ、2進~10進のバイナリアップカウンタをつくってみました。
冒頭に書いたように、verilogHDL によるシミュレーションは、論理式が正しいかどうかの確認をしているだけで、回路図には連動していません。じっさいに回路をつくっていませんので、回路図に間違いや不具合があるかもしれません。内容については保証できませんので、あしからず。
なお、間違いをみつけたら、こっそり直しておきます (;´Д`)
さて、ここまできたのですからもうひとふんばり。Dフリップフロップを使った 11進~16進カウンタもつくっておきたいと考えています。いつになるかわかりません。途中挫折もあり、です。