今回は、マルチプレクサ (セレクタ) を勉強します。
マルチプレクサとは、複数の入力から 1個を選択して出力する論理回路。詳しくは、はい、いつものようにググってください m(_ _;)m
なお、デマルチプレクサについてはこちらをご覧ください。
実験用の入出力回路
まずは、回路の実験の前に入出力の回路をつくっておきましょう。
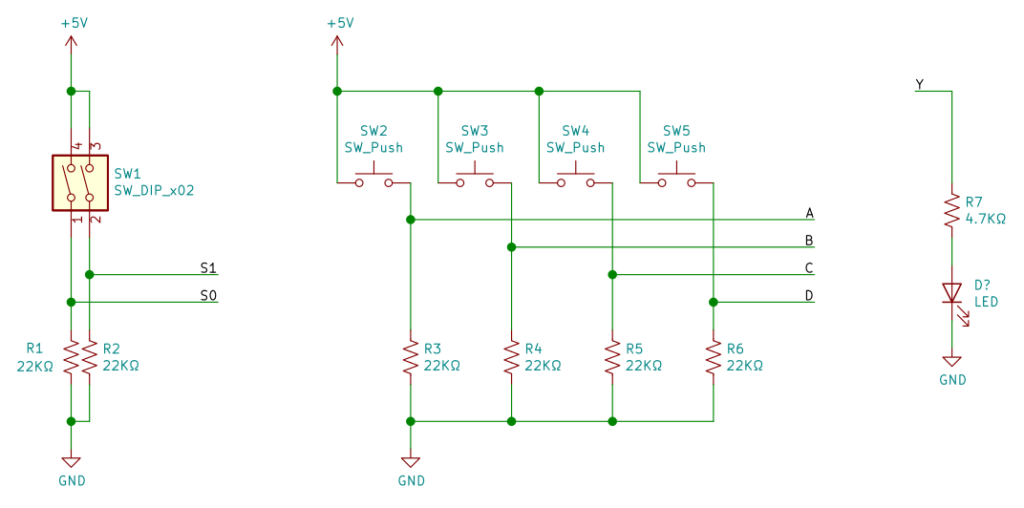
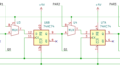
図1、説明するまでもないですが。
左がセレクト信号のスイッチ回路です。Dipスイッチで、S0、S1 の信号をだします。その右がデータ信号用の押しボタンスイッチ。A~D の信号をだします。右端が、出力 Y 表示の LEDです。
2入力マルチプレクサ
真理値表と論理式
| S0 | A | B | Y |
| 0 | 0 | x | 0 |
| 0 | 1 | x | 1 |
| 1 | x | 0 | 0 |
| 1 | x | 1 | 1 |
表1 は、2入力マルチプレクサの真理値表です。
S0 が 0 のときは、入力 A が出力される。S0 が 1 ならば、入力 B が出力される。S0 の状態によって、A、B のどちらかが選択される、という論理回路です。
真理値表から論理式をつくると、
Y = S0⋅A + S0⋅B
ちなみに、verlogHDL でのセレクタの記述は、
assign Y = (1'b1 == S0) ? B : A
です。
2入力マルチプレクサ回路
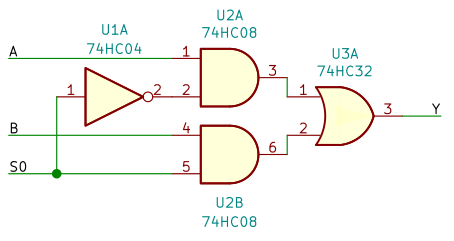
論理式を組み合わせ回路にしたのが図2 です。
教科書なんかでよくみる回路ですね。AND と OR と NOT を使う贅沢な回路だなぁと、俺は思います。
むずかしい回路ではないです。S0 によって U2A か U2B のどちらかが真になるというだけです。
NAND を使った 2入力マルチプレクサ
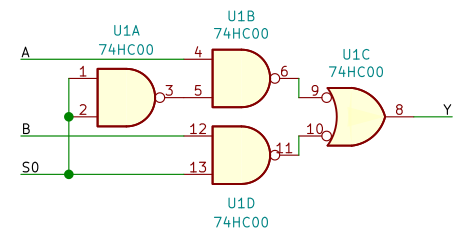
図2 の AND の出力と OR の入力に ○ をつけてみましょう。接続されたラインが負理論になるだけで、動作はかわりません。
が、AND と OR が、どちらも NANDゲートに変わってしまいます。ついでに NOT も NANDゲートを使うことにして、4回路入り NAND 74HC00 1個でつくることができました。(図3)
論理回路記号のド・モルガン変換
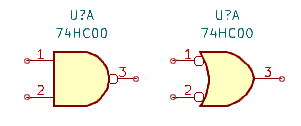
図3-1 左は正理論入力、負理論出力の AND、右は負理論入力、正理論出力の OR になっていますが、どちらも NANDゲートです。論理式は、ド・モルガンの法則により、
Y = A ⋅ B = A + B
となって、同じ論理回路であることがわかります。
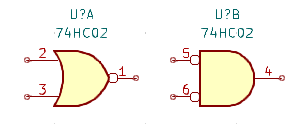
図3-2 では、左は正理論入力、負理論出力の OR、右は負理論入力、正理論出力の AND で、どちらも NORゲートです。論理式は、
Y = A + B = A ⋅ B
で、これも同じ論理回路です。
これらの論理回路は、真理値表ではそれぞれ同じになりますが、機能という点では AND または OR とみることができます。たとえば図3 の回路は、すべて NANDゲートで構成されていますが、機能としては AND と OR として働いています。
このように、論理回路記号をド・モルガン変換することで、信号の HIGH / LOW ではなく、AND か OR かという機能を、回路図から読み取ることができるようになります。
2入力マルチプレクサの動作確認
Dipスイッチで S0 をオフにしたとき、入力押ボタン A を押すと LED が点灯します。B を押しても反応しません。「反応しない」とは「点灯も消灯もしない、don’t care だ」ということです。
S0 をオンにすると、B を押したときに点灯し、A には反応しなくなります。
S0 によって、A、B のどちらかが選択されて Y に出力されることが、確認できました。
4入力マルチプレクサ
真理値表と論理式
| S1 | S0 | A | B | C | D | Y |
| 0 | 0 | 0 | x | x | x | 0 |
| 0 | 0 | 1 | x | x | x | 1 |
| 0 | 1 | x | 0 | x | x | 0 |
| 0 | 1 | x | 1 | x | x | 1 |
| 1 | 0 | x | x | 0 | x | 0 |
| 1 | 0 | x | x | 1 | x | 1 |
| 1 | 1 | x | x | x | 0 | 0 |
| 1 | 1 | x | x | x | 1 | 1 |
4入力のマルチプレクサをつくってみましょう。
表2 が、4入力マルチプレクサの真理値表です。
S0、S1 はバイナリコードとみることができます。0x0~0x3 の値に対して、入力 A、B、C、D がそれぞれ選択されて出力されます。
論理式は、
Y = S1⋅S0⋅A + S1⋅S0⋅B + S1⋅S0⋅C + S1⋅S0⋅D
これを論理回路にすると、NOT と、3入力AND、4入力OR を使った回路になります。回路図は載せませんが、ググるとでてくる一般的な回路です。(参考リンク)
うーん、なんだか複雑。
3入力AND とか部品箱にないので、論理式をちょっと変換してみました。
Y = S1⋅S0⋅A + S1⋅S0⋅B + S1⋅S0⋅C + S1⋅S0⋅D = S1(S0⋅A + S0⋅B) + S1(S0⋅C + S0⋅D)
変換した式は、「『A、B を S0 でセレクトした出力』と、『C、D を S0 でセレクトした出力』を、さらに S1 でセレクトする」という形になっていることがわかります。つまり、2入力を 3つ用意すれば、4入力マルチプレクサになる、と。
4入力マルチプレクサ回路図
ということで、つくったのが 図4 の回路です。74HC00 でつくった 2入力マルチプレクサを 3個つなげています。
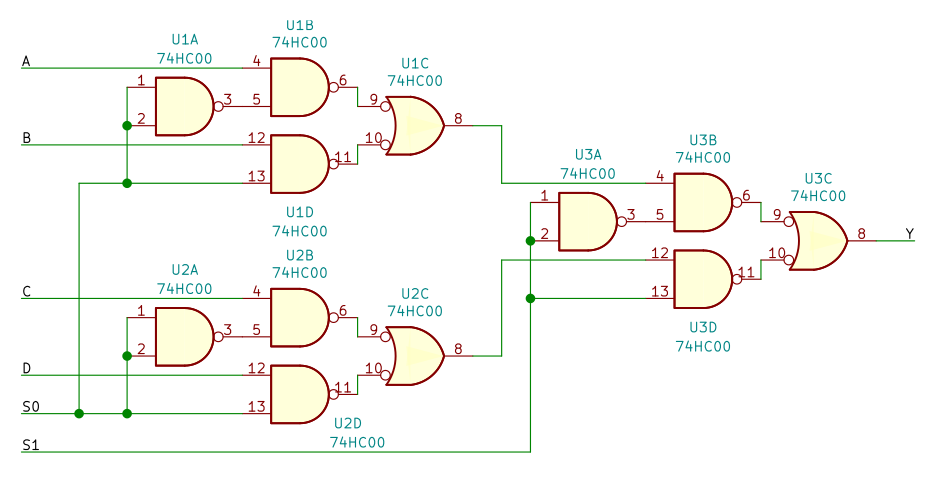
入力 A、B は S0 でどちらかが選択されます。入力 C、D も S0 で選択されます。それぞれの出力は S1 でもう一度選択され、最終的にどれかひとつの入力が出力されます。
4入力マルチプレクサの動作確認
Dipスイッチで S1、S0 ともにオフ (0x0) にすると、押しボタンA を押したときに LED が点灯します。他の押しボタンは、どれを押しても反応しません。
S0 のみをオン (0x1) にすると、B を押したときに LED が点灯。S1 のみオン (0x2) では C で、両方をオン (0x3) したときは D で点灯しました。それぞれ、他の押しボタンを押しても反応しません。
真理値表どおりの出力が得られることを確認しました。
ブレッドボード
4入力マルチプレクサの実験をおこなった、ブレッドボードのようすです。あ、パスコン、つけてないや (;´Д`)
左端が切れてますが、Dipスイッチで S0、S1 の信号をだしています。その右に、データ A、B、C、D の押しボタンスイッチ。IC は 74HC00 が 3個。右下に出力表示の LEDが見えています。
IC 1個が 2入力マルチプレクサ 1回路になってます。どれもみな同じ接続ですので、簡単。それぞれの入力、出力を回路図通りにつなげばおしまいです。
後記
今回は、2入力、4入力のマルチプレクサをつくってみました。
ググるとでてくる 4入力マルチプレクサをみて、3入力AND なんて部品箱にないなぁ、どーしよっかなぁ、と考えていました。でも、真理値表、論理式とつくってみたら、2入力の組み合わせで 4入力にできることに気がついた。
あらためてだけど、教科書だけみて理解しててもダメだなと、思ったです。
マルチプレクサの品番ですが、74HCシリーズでは、
74HC151 74HC153 74HC157 74HC158
74HC253 74HC257 74HC258
74HC354 74HC356
といったところのようです。それぞれ入力数とか機能とか違いますので、データシートみてください。
ちなみに、秋月電子通商にはどれも、ない、です (2023.7.22現在) (;´Д`)